Altitudo sonorum. La conceptualisation de la hauteur de son dans les gloses sur Martianus Capella de Jean Scot, dit l’Érigène
Violaine Anger
| PDF | CITATION | AUTRICE |
Résumé
La notion de hauteur de son, altitudo sonorum, est essentielle pour la mise au point de l’écriture musicale occidentale : elle associe un élément visuel, le haut et le bas, au son. Elle existe de façon intuitive dans l’écriture neumatique. Une convergence de faits laisse penser que le concept de hauteur de son a été élaboré au IXe siècle dans les milieux scolaires entourant Jean Scot, dit l’Érigène, sous Charles le Chauve, dans une réélaboration de la conception du monde et une réinterprétation de la science léguée par les savants de l’Antiquité.
Mots clés : analogia ; diastema ; musique des sphères ; polyphonie ; voix.
Abstract
The notion of pitch, i.e. the opposition of high and low, altitudo sonorum, is essential to the development of Western musical writing; it associates a visual element, high and low, with sound. Pitch exists in neumatic notation without conceptualization A convergence of facts suggests that the concept of musical pitch was developed in the 9th century in the schools associated with John the Scot, also known as the Eriugena, under Charles the Bald, in a re-thinking of the world view and a reinterpretation of the science bequeathed by scholars of antiquity.
Keywords: analogia; diastema; music of the spheres; polyphony; voice.
La notion de hauteur de son est essentielle dans la musique occidentale : c’est elle qui permet la notation sur ligne, et, d’une façon plus large, l’écriture de la musique polyphonique. Elle apparaît vers le IXe siècle, précédant de quelques générations d’élèves les textes d’Hucbald de Saint-Amand, ainsi que la Musica et la Scolica enchiriadis (fin IXe siècle) qui donnent les premiers exemples d’écriture musicale sur ligne. Tout converge pour situer cet intérêt dans le cercle irlandais de Laon-Corbie-Auxerre, sous Louis le Pieux et Charles le Chauve. Mais d’où vient-elle ? Cette question a été posée depuis plusieurs années et de nombreux travaux ont contribué à esquisser des réponses. Marie-Elisabeth Duchez, en particulier, a interrogé les traités de façon précise et émis l’idée que la grande figure de Jean Scot dit l’Érigène pourrait y être associée (Duchez 1979, 1980, 1981, 1987). Mariken Teeuwen, à partir de travaux sur la musique des sphères, a fait largement progresser l’enquête, comme nous le verrons (Teeuwen 2002, Teeuwen et O’Sullivan 2011). Nous voudrions ici attirer l’attention sur un texte de Jean Scot qui, dans ses gloses sur Martianus Capella, propose le concept d’altitudo sonorum, la hauteur de son. Sa façon très pédagogique d’en parler laisse envisager qu’il pourrait bien être le premier à le faire. L’intérêt de ce texte est qu’il pourrait ainsi permettre d’articuler précisément avec son système théologico-philosophique cette notion essentielle pour l’écriture musicale.
Cet Irlandais, maître de l’école du palais de Charles le Chauve, laisse une œuvre considérable dans laquelle le Periphyseon constitue l’une des premières grandes sommes occidentales de cosmologie et de philosophie de la nature. Il se situe comme un passeur essentiel de la pensée grecque, non seulement celle, antique, transmise par le Commentaire au « Timée » de Platon rédigé au IVe siècle par Calcidius, qu’il lit de près et cite, mais aussi celle, chrétienne, des Byzantins Denys l’Aréopagite qu’il traduit, et Maxime le Confesseur. On sait que les échanges culturels avec les Grecs ont été très importants pour les Carolingiens1L’utilisation du genre masculin a été adoptée afin de faciliter la lecture et n’a aucune intention discriminatoire., même si les échanges économiques l’étaient peu. Mais ce maître a également commenté pour ses élèves un texte qui s’est imposé comme une source des arts libéraux, Les noces de Mercure et de Philologie, long texte composé par le philosophe non chrétien Martianus Capella au tournant des IVe et Ve siècles2Il s’agit d’un texte pédagogique qui raconte les noces du dieu Mercure avec la mortelle Philologie et l’ascension de cette dernière vers l’apothéose, à l’aide des arts libéraux : par le savoir, de moins en moins liée à la pesanteur et à l’irrationalité terrestres, elle devient immortelle.. Les gloses de Jean Scot ont été transmises et doivent être placées dans l’ensemble des gloses sur Martianus qui commencent à être étudiées aujourd’hui, en particulier en Italie où est accompli un travail considérable (voir Scot Érigène 2006). Comme le remarquent Erika von Erhardt-Siebold et Rudolf von Erhardt (1940, p. 35), c’est un esprit mûr qui commente Martianus, et non pas celui d’un étudiant qui lui demande la vérité, une impression qui est partagée par Cora E. Lutz (1939, p. xxiii).
L’attribution sans réserve à Jean Scot de ces textes est chose faite (Erhardt-Siebold et Erhardt 1940, p. 33 ; Schrimpf 1973 ; Bischoff 2004, II, p. 359, no 3777). Un manuscrit du IXe siècle originaire de Metz intitulé Annotationes in Marcianum, aujourd’hui conservé à Oxford, est suffisamment différent du manuscrit de la Bibliothèque nationale de France (Bnf Lat. 12960) édité par Cora Lutz pour qu’Édouard Jeauneau ait estimé intéressant de le publier à part (Jeauneau 1978). Il s’achève par un bref traité de quatre pages, « Sur l’harmonie des mouvements du ciel et des sons des astres », qui est en fait une synthèse de la conception érigénienne. C’est ce texte qui nous intéresse pour notre question, dans le contexte de l’ensemble des gloses et de leurs sources3Voir annexe 2 pour une proposition de traduction..
Le mot altitudo y apparaît à plusieurs reprises. Commençons par en relever trois occurrences. Le terme semble acquis lorsque dans les gloses de L’harmonique, dernier livre des Noces consacré aux proportions musicales, Jean Scot traduit laconiquement pour ses élèves acumen par altitudo. Il transforme acumen, sommet, qui donne acutus et désigne, encore aujourd’hui, un son aigu, pointu, en haut. En d’autres termes, et sans aucun autre commentaire, il nous dit : « acuité : hauteur » (Annotationes 496-15, Lutz 1939, p. 206 ; notre traduction)4Texte de Capella : « Constat autem omnis modulatio ex gravitate soni vel acumine ». Glosé : « acumen : altitudo »..
Mentionnons également une définition dans les gloses du livre sur L’astronomie : « on parle d’altitudo quand le cercle d’une planète est élevé plus haut que la Terre5« Altitudo est quando circulus alicuius planetae altius elevatur a terra ». Jean Scot glose Martianus, Astronomie VIII, 884, qui donne lui-même déjà une définition très proche : « eius altitudo, id est ubi se eius circulus a terra altius tollit ». Scot insiste sur le mouvement là où Martianus ne voit que le cercle. » (Annotationes 467-5, ibid., p. 185 ; notre traduction). Il s’agit là d’une notion d’astronomie. Elle apparaît dans le contexte d’une description du mouvement de Mars qui passe au-dessus et au-dessous du Soleil.
Enfin, le terme explicite, mentionnant le son, d’altitudo sonorum, apparaît dans le manuscrit d’Oxford : « il y a les tons harmoniques, dont il s’agit ici, en gravité et en hauteur de son6« Sunt toni armonici, de quibus nunc agitur, in grauitate et altitudine sonorum ». » (Jeauneau 1978, p. 1277Notre traduction, comme toutes les citations à venir de ce texte édité par Jeauneau.).
Le terme altitudo dans ces gloses de Jean Scot, signifie donc à la fois l’altitude, géographique pour ainsi dire, de l’orbite, visible depuis la terre, qu’une planète dessine dans le ciel, et la hauteur sonore. S’agit-il d’homonymes ou d’une notion précise qui rejoint les deux disciplines ? Et de quoi s’agit-il si on parle de hauteur de son ? C’est ce que nous allons chercher à préciser ici. Nous devrons pour cela comprendre le contexte du modèle musical de Jean Scot, avant d’interroger de plus près le texte de référence. Cela nous amènera à tenter de situer la nouveauté de cette notion d’altitudo sonorum.
Préalable : le contexte d’une réinterprétation du monde et de la musique des sphères
Il est nécessaire auparavant d’esquisser la vision du monde que Jean Scot déploie, vision dans laquelle le son est repensé à l’intérieur d’une conception cosmologique qui, tout en empruntant beaucoup à ses sources, a une certaine originalité. Pour Jean Scot, le monde est théophanie divine. Cela entraîne plusieurs conséquences, en particulier le fait que le monde de Scot se démarque radicalement du modèle antique fabriqué à partir du modèle des nombres. Pour Platon et jusqu’à Boèce, les nombres, discontinus, sont le modèle du démiurge pour créer un monde harmonieux, voué sans cela au chaos, à l’incommensurable, à l’irrationnel (voir Institution arithmétique 1,2,1, Boèce [1995]2002, p. 11). Les nombres, et en particulier les médiétés, la science des moyennes qu’est l’harmonique, permettent de contenir le chaos, c’est-à-dire de trouver une relation entre le même et l’autre. Au contraire, dans le monde érigénien, le Démiurge, « Monade superessentielle », est radicalement transcendant, inconnaissable même par lui-même. Les nombres ne sont donc pas un modèle statique et absolu, mais une cause, une vis, une force énergétique unifiante. C’est ce que l’on va retrouver dans le son.
Jean Scot refuse également l’idée d’un monde localisé en fonction des substances, où l’eau est le lieu des poissons, l’éther celui des planètes, etc. (Periphyseon I, 475C, Scot Érigène 1995). Les quatre éléments, peut-être cinq, sont mélangés dans chaque corps, fût-il le plus immatériel. L’ensemble du monde, cosmos compris, est unifié et de nature matérielle, ceci contre une séparation dualiste entre le sublunaire et le supra-lunaire. Jean Scot revoit donc profondément les catégories établies par Aristote. Le lieu comme le temps ne sont pas des catégories parmi les autres, mais contiennent toutes les catégories restantes. Le monde avec ses parties n’est pas une multiplicité de lieux, mais il est contenu dans le lieu. Ce point est important parce que la hauteur, altitudo, sera vue (réellement vue) par la vision humaine. Elle n’a rien d’une élévation spirituelle ni d’une dématérialisation.
Le monde n’est donc pas le chaos grec. Il est une image participative d’un créateur radicalement inconnaissable dont le Verbe crée par un trop plein de bonté. Ce monde n’est pas le péché, séparé de Dieu. Dieu s’y fait au contraire connaître par une révélation silencieuse, à côté de l’Écriture. Le désordre apparent étant une production divine, il a donc sa part de beauté et les arts libéraux profanes ont toute légitimité, non pas pour aider à s’en extraire et devenir immortel, comme chez Martianus, mais pour permettre de l’admirer, d’en contempler l’ordre, même si certaines choses, comme les monstres ou l’irrationnel, peuvent nous échapper. Les nombres relèvent du Verbe et de ce que Jean Scot appelle « les causes premières », auxquelles il consacre un livre entier du Periphyseon.
Dans ce monde, le son est la première théophanie et c’est par lui qu’est assurée la relation entre sensible et intelligible (Homélie 304D, Scot Érigène [1969]2008), avant la lumière, au sens logique et non pas chronologique puisque tout a été créé en même temps. C’est la clameur de Dieu. Ce dernier n’est pas un musicien qui reproduit dans l’équilibre du monde les lois musicales de l’harmonique (ce qu’il est chez Platon ou Calcidius), mais il clame, à la façon dont la voix humaine est l’émanation sensible de la pensée intérieure qui demeure tout en se rendant extérieure et sonore. Cette clameur créatrice est donc un son continu. Et dans cette clameur divine, il y a les nombres, que le sens intérieur humain peut contempler, mais également de l’inconnaissable.
La consonance n’est donc pas le bien rationnel, c’est l’avant-goût sensible de l’harmonie qui est perçue par notre sens intérieur. Pour Pythagore ou Platon, c’est un rapport mathématique ; pour Aristoxène, elle est la manifestation sensible d’un rapport mathématique ; pour Jean Scot, c’est la substance essentielle de ce que l’on appréhende par les sens et elle relève d’un effort cognitif individuel. Le nombre est un principe énergétique fondateur et non pas un modèle à appliquer. Le sensus interior, sens cognitif propre à l’homme, nous permet de connaître les nombres et d’apprécier leurs rapports. Il le rappelle dans le Periphyseon :
Il y a là quelque chose d’admirable et que notre esprit, à lui seul, peut à peine comprendre ; ce qui produit la suavité de l’harmonie, ce ne sont pas les sons divers (par exemple ceux des tuyaux de l’orgue ; des cordes de la lyre ou des orifices de la flûte), perceptibles par nos sens et qui semblent figurer au nombre des natures, mais les rapports de sons et leurs proportions, rapports et proportions dont la convenance réciproque n’est perçue et jugée que par le sens intérieur de notre esprit.
Que celui qui écoute les sons pour découvrir ce qui en eux produit cette douceur et cette beauté parvienne à les comprendre ou ne parvienne pas à les comprendre, il n’en reste pas moins que le sens intérieur inhère à tous les sons et que l’harmonie appropriée des natures et leur unification de lui échappent pas. (Periphyseon V, 965D, Scot Érigène 1995)
Il ne s’agit pas d’échapper à notre corps pour trouver le nombre ; pas non plus d’un son qui serait la matérialisation sonore d’un rapport entre des nombres. Il faut éprouver à l’intérieur de soi-même quelque chose de l’unité qui transparaît dans le sensible. Jean Scot cite beaucoup Augustin, même si le sens intérieur n’est pas exactement le verbum in corde (voir Panaccio 1999). Il n’y a pas un choix dualiste entre le nombre ou le chaos, mais la participation de tout, même du monstrueux, à un principe unique que chacun peut appréhender à mesure de sa progression dans la compréhension du monde.
Comme l’intellect se fait connaître par la voix tout en demeurant l’intellect, le Verbe incarné est ce qui permet à l’homme de connaître le monde et d’accéder, à l’intérieur de ses limites, à la vérité. À côté de l’essence à ordonner (Platon, Aristote, Porphyre) surgissent chez Jean Scot l’existence, l’intériorité, et, grâce à l’Incarnation du Verbe qui sauve l’Humanité, l’unité de la différence, non pas par médiétés statiques, mais par compénétration réciproque. La conception globale du monde a ainsi changé. L’important est ici de comprendre l’unité dynamique et corporelle qu’est l’ensemble du cosmos ainsi que le rôle du son dans cette construction.
Rappelons que l’astronomie est, comme le dit Cassiodore, la science qui « consiste à approcher mentalement les cieux et à examiner la structure céleste en utilisant une investigation rationnelle » (Institutiones II, 6, 4, Cassiodorus 2014 ; notre traduction). À une époque où on n’a aucun autre accès à l’ordre cosmique qu’un raisonnement développant l’hypothèse de l’harmonie du monde, Jean Scot propose un cosmos où quatre planètes tournent autour du Soleil, de Jupiter, de Mars, de Vénus et de Mercure. Le Soleil tourne lui-même autour de la Terre, comme la Lune et Saturne (Periphyseon III, 698A, Scot Érigène 1995 ; Annotationes 13, 23, Lutz 1939 ; Timée 38C, Platon 1985). L’ensemble fait deux octaves, le Soleil étant l’octave intermédiaire. Sous le Soleil, vers l’aigu, Vénus, Mercure et la Lune ; au-dessus du Soleil, vers le grave, Mercure, Jupiter et Saturne (Periphyseon III, 721B, Scot Érigène 1995). Les Fixes sont le plus aigu.
Erika von Erhardt-Siebold et son mari ont précisé le modèle en montrant que Jean Scot ne recourt pas à des orbes homocentriques mais décentrés ; il n’est même pas sûr qu’il pense en orbe, mais plutôt en mouvements circulaires qui ne seraient pas attachés à des sphères solides (Erhardt-Siebold et Erhardt 1940, p. 31 ; Calcidius 2011, I, 84, p. 311), dont il ne mentionne même pas le centre (Erhardt-Siebold et Erhardt 1940, p. 17). Ce qui l’intéresse surtout, c’est la beauté d’ensemble du système (ibid., p. 42). Et, de façon beaucoup plus importante pour notre propos, Jean Scot imagine que les planètes passent au-dessus ou au-dessous du Soleil, ce que précise encore le Periphyseon (Periphyseon III, 698A, Scot Érigène 1995).
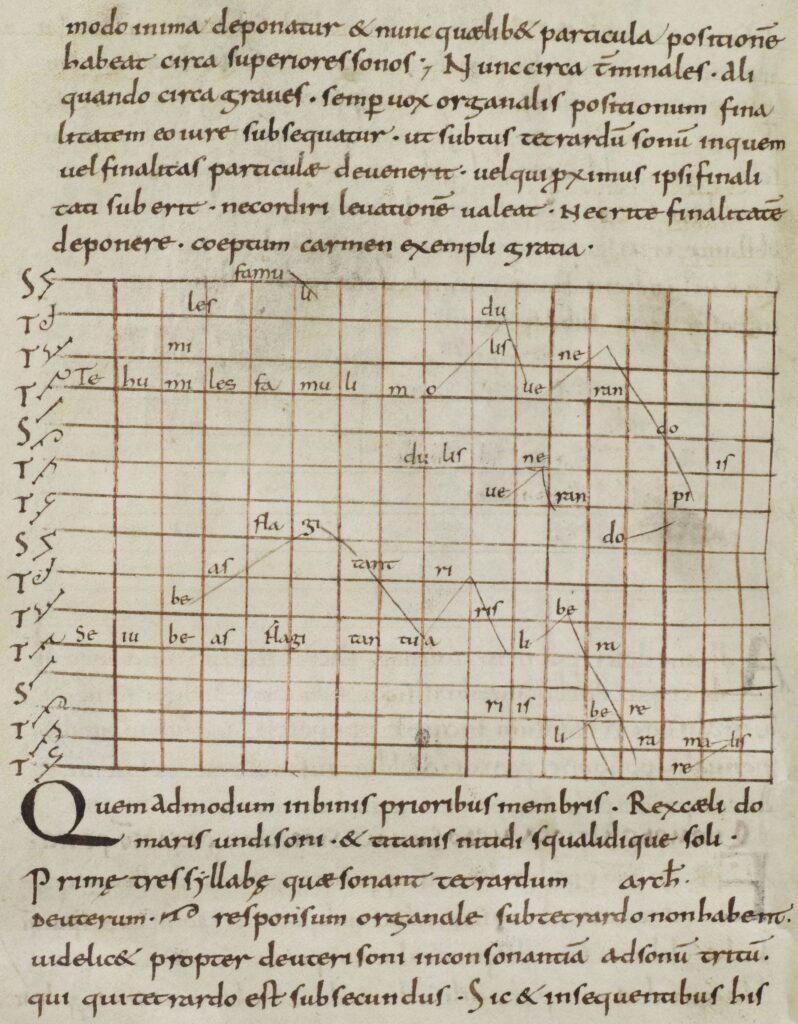
Figure 1 : Trajectoires croisées autour du Soleil (Erhardt-Siebold et Erhardt 1940, p. 9).
L’important pour notre propos est qu’il y a des points d’intersection multiples, entre le milieu ou le centre de chaque orbite, et qu’il y a un mouvement fin entre le « dessus » et le « dessous », en particulier autour du Soleil (ibid., p. 17), autant qu’un ordre géographique des planètes dans le cosmos, selon leur distance à la Terre. Du coup les distances varient, de façon impossible à calculer, mais les rapports consonants existent puisque l’ensemble est harmonieux. L’octave supérieure ou inférieure au Soleil peut devenir quarte ou quinte, et les planètes qui constituent ces intervalles peuvent parcourir tous les modes. Cela permet d’envisager la musique des sphères selon une complexité encore inconnue. Il ne s’agit plus d’ordonnancer les planètes dans un alignement, mais de comprendre l’harmonie de leur mouvement. Le nombre n’est plus un cadre statique, c’est l’explication d’une harmonie postulée comme préalable à tout.
C’est dans ce contexte que, dans les gloses sur la cosmologie de Martianus, surgit le mot d’altitudo, en particulier dans le manuscrit d’Oxford (Annotationes in Marcianum) qui va être notre guide à présent.
La musique, un modèle permettant de penser le monde
Le monde est donc bien plus complexe que le modèle d’une simple corde cosmique où l’on mesurerait des intervalles entre planètes, selon le modèle harmonique usuel qui est répandu et discuté y compris chez Boèce. Jean Scot ajoute :
Tu as à la fois un diapente [quinte] et un diatessaron [quarte] entre le Soleil et Saturne. Et tu ne t’étonneras pas que le Soleil entre en convenance avec les autres planètes par plusieurs proportions. Nous disons en effet qu’il s’emboîte de trois façons avec Saturne […]. (Jeauneau 1978, p. 125)
Il y a donc de multiples possibilités de consonances entre les planètes, et, qui plus est, elles sont variables puisque les distances des planètes entre elles sont variables.
Trois modèles musicaux permettent de penser cette cosmologie très neuve. Chercher des modèles musicaux pour penser le monde n’a rien de neuf, mais les modèles, eux, le sont. Il y a d’abord, le modèle de la corde que l’on tend, tel que décrit par Jean Scot :
Et parce […] qu’une corde placée dans un espace plus court ou plus grand, soit tendue, soit relâchée, ne rend pas le même son déterminé, bien qu’elle ne change pas de nature. […]. Le mot « ton » en effet provient de tendre ; il est grec et est dérivé du verbe teino, c’est-à-dire étendre. (Ibid., p. 128)
Intégrer ainsi la tension de la corde, en lien avec la sonorité produite, est une préoccupation omniprésente dans le texte. Le cosmos de Jean Scot est pour ainsi dire élastique, pensé à partir d’un son continu. C’est l’intégration pleine et entière de toute l’approche issue d’Aristoxène (voir Szabo 1977, p. 183). Joscelyn Godwin a relevé que Jean Scot est le seul auteur, avant Anselme et Kepler, à avoir imaginé une harmonie des sphères mobiles (Godwin 1993, p. 105).
Le deuxième modèle est celui des tuyaux de l’orgue. Il s’agit de la pratique musicale la plus nouvelle de son temps :
C’est pourquoi, de même que pour l’orgue on ne considère pas le lieu où se trouvent les tuyaux mais quel est leur son et de combien et avec lesquels ils sont reliés et quelle proportion ils réalisent ‒ et un tuyau entre en consonance avec beaucoup d’autres pour donner des symphonies diverses ‒, de même ce n’est pas le lieu des étoiles mais leur son qui compose l’harmonie céleste. (Jeauneau 1978, p. 127)
À la suite des tuyaux d’orgue, Jean Scot a recours à un troisième et dernier modèle, puissant et très neuf, celui du chant polyphonique8Teeuwen (2002, p. 333-335) a relevé cette mention incontestable de la polyphonie vocale dans le texte du maître irlandais. :
Utilisons donc un exemple pour qu’apparaisse de façon plus manifeste ce que nous cherchons à établir. Dans un chœur, où consonnent ensemble beaucoup de chanteurs, on ne considère pas le lieu où se trouve chacun mais la proportion de sa voix [avec celle des autres]. En effet, quel que soit le lieu où se trouve celui qui émet le son le plus grave, il est nécessaire que la plus grave de toutes les voix parvienne à la proportion sonore juste. Par la même raison, où qu’il se trouve dans le chœur, celui qui émet la voix la plus aiguë tiendra nécessairement le sommet de tous les sons. Il faut comprendre de la même façon que, dans ce qui suit, on ne juge pas la position locale mais l’émission vocale proportionnelle dans l’ensemble des modulations. C’est donc en vain qu’on pensera rendre la musique céleste par une proportion d’intervalles liés aux lieux. (Ibid., p. 129)
On a refusé de lire certains passages du Periphyseon comme reliés à la polyphonie, à juste titre (Coussemaker 1841, p. 123, et 1852, p. 11 ; Hanschin 1927, p. 316-341 ; Wiora 1971, p. 33-43 ; Waeltner 1977). En effet, les termes utilisés dans ces passages, en particulier celui d’organum, peuvent ne pas avoir la signification polyphonique qu’ils ont prise à partir du XIe siècle, et par ailleurs, le modèle musical sert à cet endroit à expliquer un enjeu métaphysique que l’on peut parfaitement comprendre même si une seule voix est en jeu, sans qu’il y ait besoin de recourir à la polyphonie pour expliquer ce passage. En revanche ici, l’allusion à la polyphonie est indubitable. Elle est le modèle que Jean Scot utilise pour construire sa cosmologie, une pratique savante liée à une reconsidération profonde de la nature même du son.
La place géographique des tuyaux de l’orgue et le lieu où se tiennent les chanteurs en polyphonie n’ont rien à voir avec la hauteur des sons : c’est ce point précis qui est fondateur. On écoute la musique seule et on entend les consonances. Or, ce raisonnement est essentiel : il n’est pas possible en effet de penser mesurer autrement les distances dans le cosmos, puisque la terre n’est pas une planète (même si elle est ronde) et qu’elle ne sonne pas. La distance terre-Lune, qui a été mesurée de façon assez exacte par les astronomes grecs, était généralement associée à un ton. À partir de là, on pouvait donc espérer mesurer le cosmos, de façon linéaire, à l’image de la division harmonique d’une corde, en considérant que les planètes, associées chacune à un son, étaient comme situées sur une corde, à des distances à déterminer. Jean Scot, lui, discute de l’immobilité de la Terre, en préférant parler de pesanteur ou d’impondérabilité plus que d’immobilité (Periphyseon I, 477A, Scot Érigène 1995). Dans le manuscrit d’Oxford, il utilise le fait que la terre est immobile pour réaffirmer l’impossibilité de mesurer le cosmos à partir de la distance terre-Lune :
La cause de beaucoup d’erreurs provient de l’ignorance des tons, chez ceux qui estiment que le ton par lequel la Lune est distante de la terre est pertinent pour [parler des] proportions des sons célestes, alors qu’ils ne se rendent pas compte auparavant que le ton musical est constitué de deux sons, tandis que la terre, parce qu’elle est immobile, ne produit aucun son, et que donc il n’y a pas de son musical entre la terre et la Lune. (Jeauneau 1978, p. 129)
On comprend alors que ce cosmos est mobile et sans repère fixe, que ce repère soit la terre, les centres des orbites ou la circonférence des orbes ou absides de chaque trajectoire. Altitudo désigne dans ce cas des rapports mesurables harmoniques entre planètes : il s’agit d’aborder une organisation sonore autonome, une proportion pure, sans autre repère puisqu’on ne peut pas mesurer des distances. La notion permet d’appréhender par exemple le rapport de Mars au Soleil vu depuis la terre : la planète monte et descend, mais sans qu’on ait les moyens de mesurer la distance qu’elle parcourt ou la distance qui les sépare, et cela va au-delà des possibilités humaines de calcul. Scot écrit encore :
Et ce que nous avons dit du Soleil, il faut comprendre qu’il en est de même, mutuellement, pour toutes les planètes. En effet, ce n’est pas toujours par les mêmes intervalles que soit, alternativement, elles prennent de la distance, soit, inversement, elles se rapprochent en raison de la situation de leurs absides, et ainsi, il faut croire que toutes les consonances musicales peuvent être obtenues par les huit sons célestes, non seulement dans les trois genres, diatonique, chromatique et enharmonique, mais aussi dans d’autres qui se situent hors de la capacité de calcul de tous les mortels. (Ibid., p. 126)
Pour la musique des sphères, Béatrice Bakhouche relève que, à la différence des savants antiques, « les hommes du moyen âge réussissent à donner à l’échelle de l’âme du monde des applications authentiquement musicales » (Bakhouche 2012, p. 359). On voit ici que Jean Scot y a fortement contribué.
Distinction conceptuelle entre le nombre discontinu linéaire et la proportion présente dans le continu
L’altitudo suppose que le son est un phénomène continu, contrairement à Boèce qui pense le son comme discontinu car mesurable, opposé à la voix continue (Traité de la musique, I, 12, Boèce 2004, p. 53). Surtout, il faut bien comprendre que la hauteur n’est pas une distance de corde, mais un rapport de proportions : une analogie (ana, même, logos, proportion). La hauteur de son est une proportion de proportion, une relation entre des objets mathématiques qui sont déjà une proportion, une relation proportionnelle : les sons mesurés ne sont pas d’abord des points sur la corde, mais un rapport entre deux nombres (1 à 2, 2 à 3, 3 à 4, 9 à 8). Ils peuvent éventuellement, dans un second temps, être situés sur une corde que l’on pince. Mais surtout, ils sont rapportés l’un à l’autre pour construire l’harmonie (par exemple, on peut chercher la relation qui existe entre le rapport de 2 à 3 et celui qui existe entre 3 et 4, etc., une activité que les premiers chanteurs de polyphonie ont dû pratiquer ardemment à partir des seuls résultats sonores). Il s’agit donc un pur rapport de nombres entiers, mais qui est concret et qui sonne, présent dans le monde créé, et aussi le monde visible des planètes qui sonnent même si on ne les entend pas. Ce n’est pas parce qu’on mesure que cela sonne bien, mais parce que cela sonne bien qu’on peut penser qu’il y a de la mesure, et celle-ci dépasse nos possibilités de calcul. Ceci est manifestement nouveau pour les élèves et le maître Jean Scot y revient avec insistance. Cette distinction majeure, selon laquelle il ne faut pas confondre la mesure linéaire des cordes et celle du son (nous dirions avec des repères bien différents : les centimètres ou les années-lumière et les herz), le maître est conscient qu’elle est nouvelle : il passe son temps à la répéter, non seulement dans le petit traité d’Oxford, mais dans d’autres textes. La raison qui produit l’harmonie céleste n’est pas la position des lieux mais celle des proportions sonores. Jean Scot réitère ainsi cette distinction ferme :
- « Les tons entre la terre et la Lune ne sont pas dans les proportions de voix, mais dans les lieux9« In proportionibus vocum, sed in intervallis locorum ». » (Jeauneau 1978, p. 127) ;
- « Nous ne considérons pas ici le lieu des tons, c’est-à-dire les espaces, mais les consonances de voix10« Non enim locorum tonos, hoc est spatia, hic consideramus, sed vocum consonantias ». » (ibid., p. 128) ;
- « Lorsque l’on parle de consonance dans l’harmonie céleste, il ne s’agit donc pas de la position des lieux mais des proportions des sons11« Non locorum positio sed proportionibus sonorum ratio caelestem efficit ». » (ibid., p. 124) ;
- « On juge en vain que la musique céleste est produite par la mesure des distances entre les emplacements12« Frustra igitur localium intervallorum rationibus caelestem musicam coartari arbitrantur ». » (ibid., p. 128) ;
- « Dans les orgues on ne considère pas le lieu du tuyau mais quel est son son13« Quemadmodum in organo non consideratur in quo loco sit fistula, sed qualis vox ipsius est ». » (ibid., p. 127) ;
- « Non pas la position locale mais l’émission sonore proportionnelle dans les modulations de l’univers14« Non localis positio sed proportionalis vociferatio in universitate modulaminis ». » (ibid., p. 129).
Les autres gloses le répètent : « En toutes choses, on considère non pas la position des lieux mais la proportion des voix15« In his omnibus non locorum positio sed vocum proportio consideratur ». » (ibid., p. 120).
Cette distinction est suggérée un peu plus bas dans le texte de Jean Scot d’une façon empirique. Lorsque l’on tend une corde entre deux points fixes, elle rend un certain son ; celui-ci n’est pas le même lorsque, entre les deux mêmes points fixes, on tend davantage la corde : il y a bien une différence entre la longueur de la corde et le son qu’elle rend. Il ne faut donc pas confondre un intervalle qui relève d’une distance avec celui qui relève d’un rapport entre des nombres. Sur une corde tendue graduée, qui permet de mesurer les sons, ce que l’on entend n’est pas le résultat d’une distance entre deux points de la corde, mais celui d’une relation entre des proportions de la corde.
Deux mots résument cette distinction : diastema et analogia. Diastema désigne un segment en géométrie (Szabo 1977, p. 157 ; Guillaumin 2020, p. 105). Le logos en revanche est le nom du rapport entre deux grandeurs, l’ana-logos, l’égalité entre les rapports :
Il y a en effet plusieurs espèces de tons. Lorsque les tons sont les intervalles [qui séparent] des astres, il s’agit de savoir de combien l’un est distant de l’autre. […] C’est cette espèce de ton que Martianus définit en disant : « le ton est un espace doué d’une quantité réglée (Capella, Livre XI, § 930 ; Guillaumin, 2011, p. 3016Jean-Baptiste Guillaumin traduit plus précisément par « un intervalle d’une grandeur bien définie » et insiste, dans son apparat critique, sur la polysémie du terme tonus.) ». Cette espèce est appelé diastema en musique. […] Et il y a des tons harmoniques, dont il s’agit à présent, en gravité et hauteur des sons (in gravitate et altitudine sonorum) à partir desquels est constituée toute la proportionnalité des symphonies. (Jeauneau 1978, p. 127)
C’est bien la deuxième sorte de ton qui est associée à l’altitudo. La référence à Martianus pourrait être complétée par Boèce, qui utilise le terme grec de diastema (Traité de la musique, I, 12, Boèce 2004, p. 51) : il s’agit d’une distance. Elle correspond à la mesure d’intervalles linéaires rendus par des valeurs discontinues (puisque seuls les nombres entiers sont considérés).
Jean Scot affirme qu’il faut au contraire opposer diastema et proportion ou analogia. Une à deux générations d’élèves plus tard, la Scolica enchiriadis reprendra la distinction et insistera encore en rappelant qu’il n’y a pas de silences entre les sons17« Intervallum vero est non silentii inter ptongos, sed spacii » : « l’intervalle entre les ptongues n’est pas de silence mais d’espace » (Scolica enchiriadis III, Gerbert et Schmid 1981, p. 124 ; notre traduction).. C’est une distinction très ferme qui est reprise dans le Periphyseon, avec un travail sur les notions grecques, et à nouveau dans le contexte des sphères :
Car les philosophes désignent sous le mot de ton à la fois les diastemata, c’est-à-dire les intervalles entre les sons, et les analogiae, c’est-à-dire les rapports proportionnels entre les sons (est diastemata (hoc est sonorum intervalla) et analogias (hoc est eorum proportiones)). (Periphyseon III, 715C, Scot Érigène 1995)
Tout le développement du mini-traité que nous étudions repose sur cette distinction conceptuelle nouvelle, inconnue de Boèce (voir Agmon 2013, p. 104) comme de Martianus18« Le genre diastématique doit être rattaché à la partie de la musique que l’on nomme l’harmonique » (Capella 2011, 937, p. 39). Voir annexe 1 sur le vocabulaire autour de la notion de hauteur de son.. Jean Scot insiste sur elle tout particulièrement, du fait même de sa nouveauté. On connaît depuis longtemps les rapports d’égalité, d’inégalité, on sait classer les inégalités. On sait également calculer les proportions harmoniques et elles ont sans doute occasionné la première détection des nombres irrationnels, puisque l’on a pu démontrer que ce qui manque à deux tons (rapport 9 à 8) pour faire une quarte (rapport 3 à 2) est incommensurable, c’est-à-dire qu’on ne peut pas trouver de terme commun entre les deux nombres du rapport et qu’il ne peut pas non plus devenir unité de mesure pour les autres ; en d’autres termes, qu’il n’y a pas, pour le ½ ton, de logos commun avec le reste des rapports (Szabo 1977, p. 111). La nouveauté consiste ici à considérer les rapports, non pas comme ce qui organise harmonieusement le monde continu et irrationnel, mais comme ce que celui qui écoute peut appréhender au sein de sa perception, première, d’une unité continue.
Le nombre change de statut, même si les résultats des proportions demeurent, bien évidemment. Mais il ne s’agit plus de savoir comment faire apparaître un peu d’harmonie dans ce monde chaotique, que ce soit dans les volumes ou dans tout ce qu’on peut mettre en rapport, en touchant la question du demi-ton irrationnel et en l’écartant de l’harmonie. Le nombre n’est pas, grâce à l’artifice du calcul des moyennes, ce qui permet de réduire le même et l’autre en quantifiant des types acceptables de mélange, ce que fait Platon pour expliquer la création du monde. Ici, il s’agit de comprendre qu’en toute chose, il peut y avoir proportion, c’est-à-dire un rapport. Le calcul de ces rapports se fait à présent indépendamment des endroits où ils apparaissent : le son devient lieu de la pure proportion. Le son harmonieux n’est pas le résultat d’un rapport de nombres ; il le fait apparaître, par la proportion qui le rattache à l’unité continue. Le demi-ton n’est plus l’irrationnel enserré dans des rapports rationnels, mais le résultat de l’intervalle d’un ton qui est resserré parce que le mouvement des planètes les rapproche. La proportion, l’analogie, est la marque de sa participation à l’unité continue du monde. Le nombre n’est pas ce qui ordonne le monde, il est ce que je peux y détecter grâce à mon activité cognitive. Et le monde est d’abord du son, c’est-à-dire un ensemble continu.
Or, l’altitudo sonorum est liée aux analogias et non pas aux diastemata ; elle est liée à la vision des parcours des orbes les uns par rapport aux autres, orbes que l’homme peut appréhender par sa perception de la consonance sonore parce qu’ils sont liés au son, c’est-à-dire à la clameur divine. Après la définition du ton, Jean Scot va en effet mesurer la hauteur sonore, en séparant les résultats de la pure proportion et celle qui mesure des distances. On retrouve une dernière fois cette distinction qui traverse tout le texte : toutes ces répétitions prouvent sans doute que le maître doit insister auprès de ses élèves en raison du caractère novateur de cette pensée :
Il en résulte que jamais les intervalles musicaux ne sont mesurés en nombre de stades (stadiorum numero) mais par la seule ascension raisonnable de l’extension, selon les règles des nombres (secundum regulas numerorum). C’est une chose en effet de mesurer 126 000 stades entre la terre et la Lune, et une autre chose que de mesurer la différence entre le nombre 192 et 216, soit 24 unités. Là, le ton fait 126 [000] stades ; ici, le ton fait 24, la huitième partie du plus petit nombre. (Jeauneau 1978, p. 129)
La distance entre la terre et la Lune est de 126 000 stades : c’est une distance que l’on trouve également chez Pline (Histoire naturelle, Pline 1950, II, p. 83-84)19Voir à ce sujet Freyburger 1996, p. 283-292. Ces mesures ont été sévèrement critiquées par Pierre Duhem qui voit chez Jean Scot un prédécesseur de l’astronome Tycho Brahe (avec l’idée que quatre planètes tournent autour du Soleil), mais qui néglige son système de pensée (Duhem 1913-1959, III, p. 62)., et elle sert de point de départ au calcul des distances dans le cosmos, à partir de l’hypothèse selon laquelle, celui-ci étant harmonieux, l’intervalle entre la terre et la Lune équivaut à un ton. Jean Scot revient longuement sur cette question dans le Periphyseon (Periphyseon III, 716A et 719, Scot Érigène 1995), et, nous l’avons vu, c’est pour lui un ton diastématique.
Le nombre 24, sans unité de mesure, est évidemment très opposé à celui de 126 000 stades. C’est la manière la plus simple de calculer le rapport 9 à 8, c’est-à-dire le ton, avec des entiers. On prend les premiers nombres sur lesquels on peut réécrire le rapport pour tomber sur des nombres entiers : en l’occurrence, en multipliant 9 et 8 par 24 (= 3 x 2 x 2), on obtient le même rapport, 216 à 192. 24 est le multiplicateur ; c’est aussi le résultat de la soustraction entre 216 et 192, puisque 9 – 8 = 1 donc 216 – 192 = 1 x 24. On pourrait, par le même raisonnement, multiplier 9 et 8 par 27 et on tomberait sur le rapport 216 à 243.
C’est un raisonnement que Jean Scot emprunte à Calcidius, dans le prolongement du Timée de Platon, très précisément à son troisième diagramme. Ce traducteur du IVe siècle propose en effet trois diagrammes pour résumer la pensée platonicienne du nombre, modèle de l’harmonie du monde. C’est dans le dernier diagramme que l’on trouve le nombre 24 dont parle Jean Scot.
Jean Scot donne donc ici des mesures qui lui permettent d’affermir une dernière fois la différence conceptuelle entre les diastemata (le « ton » terre-Lune qui fait 126 000 stades) et les analogias (la proportion entre 9 et 8, soit entre 216 et 192). Le « ton » qui mesure la terre à la Lune n’a donc rien à voir avec le rapport qui définit le ton harmonique : 126 000 stades n’est pas 24, même si on parle dans les deux cas d’un « ton ». De fait, nous savons bien aujourd’hui que la loi d’augmentation des fréquences est logarithmique.
Cela montre clairement aussi la nature du ton : 24 ne veut rien dire de concret, d’autant que 27 peut aussi décrire le même rapport. C’est une image mentale intérieure, ce dont Hucbald de Saint-Amand tirera des conséquences d’apprentissage très concrètes pour les apprentis musiciens, un apprentissage qui « ne demande pas peu de temps » (Chartier 1995, p. 136-137), en leur demandant d’intégrer cognitivement ce qu’est un ton sonore, par des exercices d’audition intérieure. Ceci est d’autant plus logique que Jean Scot n’est pas certain de la nature effectivement sonore du cosmos pour une oreille humaine.
Enjeux épistémologiques de cette conceptualisation
Ainsi la hauteur, notion visuelle appliquée au son, est élaborée à partir d’une homologie (le son-les planètes) fondée sur une cosmologie qui repose sur l’unification du cosmos par ses causes. Le maître Jean Scot nous invite alors à un voyage extraordinaire, selon l’organisation des sons et non plus selon la géographie : on pourrait considérer que c’est sa réponse au mythe d’Er de Platon (La République, 617c-d)20Le Pamphylien Er raconte un voyage que nous pourrions appeler « chamanique » dans le cosmos. Il y a vu en particulier les planètes tourner autour du fuseau de la nécessité, avec, assise sur chaque planète, une sirène qui émet un son.. Nous pouvons voyager dans le cosmos, non pas d’une façon plus ou moins chamanique comme le Pamphylien Er, mais par une réinterprétation rationnelle et grâce au sens intérieur :
En effet, lorsque nous commençons rationnellement par le plus grave de tous les sons, à savoir Saturne, et, par une ascension proportionnelle, nous montons jusqu’à la médiété du son solaire et que, étendant le rapport dans la partie supérieure, nous parvenons au son le plus aigu de toutes les planètes, celui de la Lune, ‒ ce qui est justifié car cette dernière occupe la plus étroite de toutes les zones de passage ‒, là où nous ne pouvons pas monter plus haut, le rapport nous a menés au mouvement de la sphère céleste, le plus aigu de tous les sons, et de la sorte nous avons joint le plus aigu de tous les sons planétaires au son le plus aigu et le plus éloigné du mouvement du monde entier, par le [seul] rapport du ton. (Jeauneau 1978, p. 128)
En d’autres termes, pour suivre toute la gamme céleste du grave à l’aigu, il faut commencer très loin et très haut par Saturne (grave), descendre jusqu’au Soleil (la médiante), puis jusqu’à la Lune (aiguë), et ensuite remonter encore plus haut aux Fixes (les plus aiguës). Ce voyage descend géographiquement vers la terre alors que le son monte du grave à l’aigu ; il est géographiquement discontinu, passant directement de la Lune aux Fixes, alors que la montée sonore est continue.
Jean Scot utilise les noms (ascensio), les verbes (ascendere) et les adverbes (altius, superius) pour exprimer un voyage dans le son, selon la proportion analogique. Ce n’est pas un voyage géographique, mais une montée sonore. Jean Scot distingue précisément ce que Martianus confondait21Voir annexe 1 sur altitudo. : il parle explicitement d’une « ascension proportionnelle », c’est-à-dire d’une ascension par les sons, mesurée, alors que l’on descend géographiquement, dans l’espace ; le concept précis de la hauteur de son naît ici.
Cela montre aussi, de façon extraordinaire, un cosmos unifié par le son, homogène, sans strates ontologiques différentes. Ce voyage intersidéral et musical n’est ni chamanique, ni psychopompe. Le son homogénéise l’ensemble de l’univers comme s’il était fait de plusieurs cordes tendues de façon différentes par les élans de chaque planète ; on appréhende les sons indépendamment des distances entre les planètes et sans avoir besoin d’être une âme : la seule rationalité humaine permet de saisir un cosmos profondément unifié.
En revanche cette notion d’altitudo, hauteur de son, est ambiguë. Elle permet certes d’imaginer de mesurer le cosmos, mais on est immédiatement tenté de se demander à quelle distance correspondent ces proportions. En fait, Jean Scot cherche ici à mesurer des distances d’arcs de cercle en mouvement : on peut comprendre qu’il n’avait pas les moyens mathématiques de le faire à son époque. Une autre question surgit donc pour nous : quand a-t-on distingué clairement l’altitude et la hauteur de son ? Il faut sans doute chercher autour du moment où l’on a commencé à distinguer les notions de longitude et de latitude de celle de durée.
Dans tous les cas, la conceptualisation de la hauteur associée à une différence conceptuelle claire entre la distance et la proportion donne la possibilité d’imaginer une autre géométrie du ciel que celle de la distance linéaire. Le déplacement conceptuel opéré par Jean Scot aurait-il permis de susciter de grands défis mathématiques aux arithméticiens à venir ? Participerait-il de façon incisive à la grande aventure cosmologique humaine ?
La hauteur de son est donc une transformation du nombre en musique : elle en fait le lieu du continu, en opposant le haut et le bas et en ne considérant que la proportion, le rapport existant entre deux notions quantitativement opposées. Elle naît d’une transformation de la cosmologie. Elle quantifie des qualités. Elle permet de situer deux objets l’un par rapport à l’autre, dans un mouvement. Elle fait se rejoindre de manière conceptuellement maîtrisée les disciplines de l’astronomie et de l’harmonique, contre l’ordonnance disciplinaire usuelle, chère encore à Boèce, qui unissait l’arithmétique à l’harmonique, sciences du nombre discontinu, et la géométrie à l’astronomie, sciences de la grandeur et du mouvement, ces dernières sciences étant beaucoup plus difficiles à fonder parce qu’elles recourent à la vue en plus du nombre et qu’elles travaillent en fait sur l’irrationnel qu’elles ne conceptualisent pas (voir Michel 1960, p. 493 sq.). Avec la hauteur de son et la musique, le continu s’invite, à plus ou moins long terme, dans l’arithmétique22Ce que dira explicitement la Scolica enchiriadis (troisième partie)..
Cette conception nouvelle de la musique et des sphères a des enjeux métaphysiques et théologiques importants. C’est ce que développe la fin du mini-traité, qui s’achève par une longue diatribe contre les Platoniciens23Cette diatribe se retrouve aussi dans les Annotationes, 13, 1, Lutz 1939, glose de « Hi igitur cursu ».. Dans nos lectures de Platon, nous avons pris l’habitude de séparer les calculs des proportions sonores et leurs implications ontologiques ; mais les élèves de Jean Scot les reliaient tellement qu’il n’est pas même nécessaire d’expliquer pourquoi il faut les mentionner : il est clair que la réorganisation du son et du cosmos qu’ils ont suivie pas à pas avec leur maître est en fait une prise de position théologique. Les âmes de Martianus Capella cherchent la connaissance des arts libéraux pour se libérer de l’entrave incohérente et vouée à la destruction des corps où elles descendent. De plus, le démiurge platonicien, tout comme celui de Boèce au demeurant, crée le monde les yeux fixés sur le nombre. Dans ce cas, seul le nombre peut expliquer l’harmonie, physique autant que psychique. C’est une conception évidemment inacceptable pour un penseur qui cherche à fonder l’existence humaine et la liberté. On voit aussi l’un des enjeux métaphysiques de cette approche de la musique des sphères : s’affranchir de toutes les superstitions liées au séjour des âmes dans les astres et s’affranchir d’une croyance en l’impact immédiat du nombre.
La science occidentale a dû oublier la musique des sphères et le rêve d’harmonie du monde qui la sous-tend ; mais on voit ici, dans son élaboration conceptuelle rigoureuse, de quels imaginaires ce rêve d’harmonie cosmique musicale se sépare, à la fois dans le rapport au nombre, au rôle donné à la proportion dans la conduite de l’harmonie du monde, et dans le statut du son. Pythagore et Platon ont permis de sortir du mythe d’Er et de la croyance qu’un voyage chamanique peut faire rencontrer les esprits, d’une foi en l’efficacité magique des sons, en affirmant que c’est le nombre, c’est-à-dire la rationalité, qui articule les mondes ; mais Jean Scot nous délivre de cet impératif d’une proportion numérique objective pour trouver l’harmonie, qu’elle soit entre les âmes, dans les caractéristiques des corps ou dans l’harmonie de la société. Il nous délivre de tout ce que la proportion considérée comme un absolu peut avoir d’emprisonnant, en insistant sur l’activité sensible qui permet à chacun de les détecter et, selon son avancée dans la connaissance, d’en rendre compte. Le rêve d’harmonie du monde est porté à une sorte de sommet tout en éliminant toute considération psychopompe. Jean Scot nous délivre d’un rapport magique à la musique et au son, et il ouvre grand l’espace cognitif du sens intérieur. C’est l’un des enjeux majeurs de la polyphonie.
Conclusion
Ainsi, ce texte du manuscrit d’Oxford sur la musique des sphères est l’une des premières sinon la première mention de la pratique polyphonique savante occidentale, ce qu’a déjà vu Teeuwen (2002, p. 333-335). La notion de hauteur de son est clairement élaborée dans les gloses sur Martianus, ce qu’avait déjà pressenti Duchez (1979, 1980, 1981). Ce texte la fait comprendre dans l’activité vivante de son affinement par l’acte pédagogique de transmission. Un faisceau de convergences permet de penser que Jean Scot dit l’Érigène en est l’initiateur : on ne la trouve pas avant lui ; elle est absolument cohérente avec toute sa métaphysique ; et il insiste beaucoup sur la distinction conceptuelle nécessaire pour l’élaborer et sur sa nouveauté.
Jean Scot pratique une synthèse qui puise à Platon transmis par Calcidius comme à Aristote (pour les catégories), à Martianus Capella comme à Boèce, Pline ou Macrobe. C’est une autre conception de l’harmonie, directement liée au nombre et à la proportion, indépendamment des objets matériels dans lesquels on les trouve. Le son est ici dégagé des distances : il est appréhendé comme un continu, une vague, un mouvement, au sein duquel, grâce aux consonances dont il est porteur, on entendra l’harmonie. Scientifiquement, c’est peut-être la première quantification des qualités (aigu et grave deviennent les opposés d’un continu). Ontologiquement, la question de l’analogie va avoir de grands et beaux jours, jusqu’à saint Thomas d’Aquin. Surtout, c’est une manière d’associer l’audible (le son) et le visible (la hauteur) qui induit un nouveau rapport à la matière dont il faudrait interroger plus avant l’originalité.
On voit que la conceptualisation de la hauteur de son relève d’une toute autre démarche que celle de sa pratique accentuelle dans l’écriture neumatique qui se développe au cours du dernier tiers du IXe siècle. Mais le concept est absolument nécessaire pour imaginer, au seuil du siècle suivant, l’écriture de la musique sur ligne (voir Rankin 2018).
La question de l’écriture de la musique en sort à la fois située et complexifiée. On comprend aussi que l’appellation usuelle de « notation diastématique » pour parler de l’écriture sur ligne n’est sans doute pas pertinente : produit d’un effet de savoir du XIXe siècle, elle est en fait un contresens, parce qu’elle désigne des intervalles discontinus. Il vaudrait mieux parler d’écriture analogique, opposée à une écriture alphabétique (pratiquée par Boèce ou plus tard Volpiano) que l’on pourrait aussi appeler numérique. Les premières écritures polyphoniques émanent de quelques traités originaires des mêmes lieux que ceux où Jean Scot a enseigné. Hucbald de Saint-Amand, l’auteur du plus ancien d’entre eux, semble avoir été l’élève d’un élève de Jean Scot24Jean Scot semble avoir été professeur d’Heiric d’Auxerre, lui-même professeur de Rémi d’Auxerre et de Hucbald de Saint-Amand, auteur du De Musica où l’on trouve pour la première fois l’écriture sur ligne. Voir à ce propos Jones 1957, p. 86 et 95, qui lui-même s’appuie sur les citations transcrites par Kenney 1929, tome 1, p. 592. Jean Scot a été aussi professeur de Martin de Laon, dont les gloses sont beaucoup moins importantes (Jones 1957, p. 102). Percy Jones ne trouve aucun lien entre les gloses sur Martianus de Jean Scot et les textes de la même famille (rattachés à l’Enchiriadis) à part l’analyse typologique d’Orphée et Eurydice, alors qu’il en … Continue reading.
Figure 2 : Cambridge, Corpus Christi College, MS 260. Musica Hogeri. Musica enchiriadis. Scholica enchiriadis. Commemoratio brevis. Fol. 15 v. Copié fin Xe siècle, Christ Church, Canterbury.
Or, à l’époque, circulent, de façon beaucoup plus vaste, mais d’origine insulaire semble-t-il, des diagrammes notant la position des astres dans le zodiaque, dans les écrits sur le comput de Bède le Vénérable.
Figure 3 : Bède le Vénérable, De temporum ratione (« Le calcul du temps », 725), British Library, Royal MS 13 A XI, f. 143v.
L’air de famille qui les réunit suscitera peut-être d’autres travaux.
Bibliographie
Sources
1. De Jean Scot
Jeauneau, Édouard (éd.) (1978), « Le commentaire érigénien sur Martianus Capella (De nuptiis, Lib I) d’après le manuscrit d’Oxford (Bodl. Libr. Auct. T. 2. 19, fol. 1-31) », dans Quatre thèmes érigéniens, Conférence Albert-Le-Grand 1974, Montréal, Institut d’études médiévales Albert-Le-Grand ; Paris, Vrin, p. 91-166, https://doi.org/1866/23050.
Lutz, Cora E. (éd.) (1939), Johannis Scotti Annotationes in Marcianum, Cambridge, Massachussetts, The Mediaeval Academy of America.
Scot Érigène, Jean ([1969]2008), Homélie sur le prologue de Jean, introduction, texte critique, traduction et notes d’Édouard Jeauneau, Turnout, Brepols.
Scot Érigène, Jean ([1972]1999), Commentaire sur l’Évangile de Jean, introduction, texte critique, traduction, notes et index d’Édouard Jeauneau, Paris, Le Cerf.
Scot Érigène, Jean (1995), De la division de la nature. Periphyseon, introduction, traduction et notes par Francis Bertin, plusieurs volumes, Paris, PUF.
Scot Érigène, Jean (2006), Tutti i commenti a Marziano Capella (2006), presentazione di Giovanni Reale, introduzione, traduzione, note e apparati di Ilaria Ramelli, Milan, Bompiani.
Sheldon-Williams, Inglis P., et Ludwig Bieler (éd.) (1968), Johannis Scotti Eriugenae Periphyseon (De Divisione Naturae), plusieurs volumes, Dublin, Dublin Institute for Advanced Studies.
2. Autres sources
Bischoff, Bernhard (2004), Katalog der festländischen Handschriften des neunten Jahrhunderts, Wiesbaden, Harassowitz.
Boèce ([1995]2002), Institution arithmétique, texte établi et traduit par Jean-Yves Guillaumin, Paris, Les Belles lettres.
Boèce (2004), Traité de la musique, introduction, traduction et notes par Christian Meyer, Turnhout, Brepols.
Calcidius (2011), Commentaire au « Timée » de Platon, édition critique, traduction française, notes sur la traduction et le « Commentaire » de Calcidius et annexes par Béatrice Bakhouche, 2 vol., Paris, Vrin.
Cassiodorus (2014), Institutiones divinarum et saecularium litterarum, Einführung in die geistlichen und weltlichen Wissenschaften, introduction, traduction et commentaire d’Andreas Pronay, Hildesheim, Georg Olms Verlag.
Capella, Martianus (2001), Le Nozze di Filologia et Mercurio, Introduzione, traduzione, commentario e appendici di Ilaria Ramelli, Milano, Bompani.
Capella, Martianus (2011), Les noces de Philologie et de Mercure, tome IX, Livre IX. L’harmonie, texte établi et traduit par Jean-Baptiste Guillaumin, Paris, Les Belles lettres.
Capella, Martianus (2014), Les noces de Philologie et de Mercure, tome I, Livre I, texte établi et traduit par Jean-Frédéric Chevalier, Paris, Les Belles lettres.
Chartier, Yves (1995), L’œuvre musicale d’Hucbald de Saint-Amand. Les compositions et le traité de musique, Paris, Bellarmin, https://doi.org/1866/22994.
Gerbert, Martin, et Hans Schmid (1981), Musica et Scolica enchiriadis, una cum aliquibus tractulis adjunctis, München, Verlag der Bayerischen Akademie der Wissenschaften.
Isidore de Séville (2009), Etymologies, Livre III. De mathématica, texte établi par Giovanni Gasparotto avec la collaboration de Jean-Yves Guillaumin, traduit et commenté par Guillaumin, Paris, Les Belles lettres.
Platon (1973), La République, texte traduit par Émile Chambry, Paris, Les Belles lettres.
Platon (1985), Le Timée, traduction et notice d’Albert Rivaud, Paris, Les Belles lettres.
Pline (1950), Histoire naturelle, texte établi, traduit et commenté par Jean Beaujeu, Paris, Les Belles lettres.
Littérature secondaire
Agmon, Eytan (2013), « Proto-Tonal Theory. Tapping into 9th-Century Insights », Music Theory Spectrum, vol. 35, no 1 (avril), https://doi.org/10.1525/mts.2013.35.1.103.
Bakhouche, Béatrice (2012), « Lectures médiévales de l’harmonie musicale de l’âme selon Platon (Timée 35b-36b). L’influence de Calcidius », dans Revue de Musicologie, tome 98, no 2, p. 339-362.
Ball, Nicholas (2019), Music, Number and Logic in Eriugena’s Reading of Augustine’s Musica, thèse de doctorat, Université de Cambridge, https://doi.org/10.17863/CAM.64114.
Coussemaker, Edmond de (1841), Mémoire sur Hucbald et sur ses traités de musique, Paris, J. Techener.
Coussemaker, Edmond de (1852), Histoire de l’harmonie au Moyen-Âge, Paris, V. Didron.
Currie, Gabriela (2008), « Concentum celi quis dormire faciet? Eriugenian Cosmic Song and Carolingian Planetary Astronomy », dans David Cannata et al. (dir.), Quomodo Cantabimus canticum? Studies in Honor of Edward H. Roesner, Middleton, American Institute of Musicology, p. 15-36.
Duchez, Marie-Elisabeth (1979), « La représentation spatio-verticale du caractère musical grave-aigu et l’élaboration de la notion de hauteur de son dans la conscience musicale occidentale », Acta Musicologica, vol. 51 (janv.-juin), p. 54-73.
Duchez, Marie-Elisabeth (1980), « Jean Scot Érigène, premier lecteur du De institutione musica de Boèce ? », dans Werner Beierwaltes (dir.), Eriugena. Studien zu seinen Quellen, Heidelberg, Winter, p. 165-187.
Duchez, Marie-Elisabeth (1981), « Description grammaticale et description arithmétique des phénomènes musicaux. Le tournant du IXe siècle », dans Wolfgang Kluxen (dir.), Sprache und Erkenntnis im Mittelalter, Berlin/Boston, De Gruyter, p. 561-579, https://doi.org/10.1515/9783110837711.561.
Duchez, Marie-Elisabeth (1982), « La représentation de la musique. Information d’action et expression structurelle dans la représentation graphique occidentale traditionnelle », dans Actes du XVIIIe Congrès des Sociétés de philosophie de langue française. Strasbourg, juillet 1980, Paris, Vrin, p. 178-182.
Duchez, Marie-Elisabeth (1983), « Des neumes à la portée. Élaboration et organisation rationnelle de la discontinuité musicale et de sa représentation graphique, de la formule mélodique à l’échelle monocordale », Revue de musique des universités canadiennes, no 4, p. 22-65, https://doi.org/10.7202/1013897ar.
Duchez, Marie-Elisabeth (1987), « Des neumes à la portée », Michel Huglo (dir.), Actes de la table ronde du cnrs à l’Institut de Recherche et d’Histoire des Textes, 6-7 septembre 1982, Paris, Champion, p. 57-60.
Duchez, Marie-Elisabeth (1989), « Le savoir théorico-musical carolingien dans les commentaires de Martianus Capella. La tradition érigénienne », dans Giovanni Scoto nel suo tempo, l’organizzazione del sapere in età carolingia. Atti del XXIV Convegno storico internazionale, Todi, 11-14 ottobre 1987, Spoleto, Centro italiano di studi sull’alto medioevo, p. 553-592.
Duhem, Pierre (1913-1959), Le système du monde, histoire des doctrines cosmologiques de Platon à Copernic, Paris Hermann ; en particulier le tome III, La physique de Jean Scot Érigène.
Eastwood, Bruce S. (1989), Astronomy and Optics from Pliny to Descartes. Texts, Diagrams and Conceptual Structure, London, Variorum Reprints.
Eastwood, Bruce S. (1992), « Heraclides and Heliocentrism. Texts, Diagrams, and Interpretations », Journal for the History of Astronomy, vol. 23, no 4, p. 233-260, https://doi.org/10.1177/002182869202300401.
Eastwood, Bruce S. (1993), « Plato and Circumsolar Planetary Motion in the Middle Ages », Archives d’histoire doctrinale et littéraire du Moyen-Âge, vol. 60, p. 7-26, https://www.jstor.org/stable/44403881, consulté le 13 septembre 2023.
Eastwood, Bruce S., et Gerd Grasshoff (2004), Planetary Diagrams or Roman Astronomy in Medieval Europe ca 800-1500, Philadelphie, American Philosophical Society, https://doi.org/10.2307/20020363.
Erhardt-Siebold, Erika von, et Rudolf von Erhardt (1940), Cosmology in the Annotationes in Marcianum. More Light on Erigena’s Astronomy, Baltimore, The Waverly Press.
Freyburger, Gérard (1996), « L’harmonie des sphères calculée en stades », dans Béatrice Bakhouche, Alain Moreau et Jean-Claude Turpin (dir.), Les astres. Actes du colloque international de Montpellier, 23-25 mars 1995, tome 1, Les astres et les mythes. La description du ciel, Montpellier, Publications de la recherche, p. 283-292.
Godwin, Joscelyn (dir.) (1993), The Harmony of the Spheres. A Sourcebook of the Pythagorean Tradition in Music, Rochester, Vermont, Inner Traditions International.
Guillaumin, Jean-Yves (2020), Dictionnaire de la terminologie latine ancienne de l’arithmétique et de la géométrie, Paris, Les Belles lettres.
Hanschin, Jacques (1927), « Die Musikanschauung des Johannes Scotus (Erigena) », Deutsche Vierteljahresschrift für Literaturwissenschaft und Geistesgeschichte, vol. 5, p. 316-341.
Jones, Percy (1957), The Glosses « De Musica » of John Scottus Eriugena in the MS lat. 12960 of B. N. Paris, Rome, Institut Pontifical de Musique Sacrée.
Kenney, James (1929), The Sources for the Early History of Ireland, tome 1, New York, Columbia University Press.
Leonardi, Claudio (1986), « Martianus Capella et Jean Scot. Nouvelle présentation d’un vieux problème », dans Guy-H. Allard (dir.), Jean Scot écrivain, Paris, Vrin, p. 187-207.
MacInnis, John (2014), « The Harmony of All Things ». Music, Soul, and Cosmos in the Writings of John Scottus Eriugena, Dordt Digital Collections, https://digitalcollections.dordt.edu/faculty_work/70/, consulté le 13 septembre 2023.
McKitterick, Rosamond (1992), « Knowledge of Plato’s Timaeus in the Ninth Century. The Implications of Valenciennes, Bibliothèque Municipale MS 293 », dans Haijo Jan Westra (dir.), From Athens to Chartres. Neoplatonism and Medieval Thought. Studies in Honour of Édouard Jeauneau, New-York, E. J. Brill, p. 85-95, https://doi.org/10.1163/9789004451902_011.
Michel, Paul-Henri (1960), De Pythagore à Euclide, Paris, Les Belles lettres.
Münxelhaus, Barbara (1977), « Aspekte der Musica Disciplina bei Eriugena », dans Jean Scot Érigène et l’histoire de la philosophie, Paris, Éditions du cnrs, p. 253-262.
O’Meara, John J. (1989), Pythagoras Revived. Mathematics and Philosophy in Late Antiquity, Oxford, Clarendon Press.
O’Meara, John J. (1990), « The Metaphysical Use of Mathematical Concepts in Eriugena », dans Werner Beierwaltes (dir.) Begriff und Metapher. Sprachform des Denkens bei Eriugena?, Heidelberg, Carl Winter, p. 142-148.
O’Meara, John J., et Ludwig Bieler (dir.) (1973), The Mind of Eriugena, Dublin, Irish University Press.
Niemöller, Klaus W. (1998), « Die Musik im Weltbild des Johannes Scotus Eriugena », dans Frank Hentschel (dir.), Musik und die Geschichte der Philosophie und Naturwissenschaften im Mittelalter. Fragen zur Wechselwirkung von « Musica » und « Philosophia » im Mittelalter, Leiden, Brill, p. 293-304.
Panaccio, Claude (1999), Le discours intérieur. De Platon à Guillaume d’Ockham, Paris, Le Seuil.
Phillips, Nancy C. (1984), Musica and Scolica Enchiriadis. The Literary, Theoretical and Musical Sources, thèse de doctorat, New York University.
Rand, Edward Kennard (1939), « How Much of the Annotationes in Marcianum is the Work of John the Scot? », Transactions and Proceedings of the American Philological Association, vol. 71, p. 501-523, https://doi.org/10.2307/283140.
Rankin, Susan (2018), Writing Sounds in Carolingian Europe. The Invention of Musical Notation, Cambridge, Cambridge University Press.
Schrimpf Gangolf (1973) « Zur Frage der Authentizitàt unserer Texte von Johannes Scottus Annotationes in Martianum », dans John J. O’Meara et Ludwig Bieler (dir.), The Mind of Eriugena, Dublin, Irish University Press.
Shanzer, Danuta, (1986), A Philosophical and Literary Commentary on Martianus Capella’s « De nuptiis Philologiae et Mercurii », vol. 1, Berkeley, University of California Press.
Szabo, Arpad (1977), Les débuts des mathématiques grecques, traduit de l’allemand par Michel Federspiel, Paris, Vrin.
Teeuwen, Mariken (2002), Harmony and the Music of the Spheres. The Ars Musica in Ninth-Century Commentaries on Martianus Capella, Leiden, Brill.
Teeuwen, Mariken, et Sinéad O’Sullivan (dir.) (2011), Carolingian Scholarship and Martianus Capella. Ninth-Century Commentary Traditions on De Nuptiis in Context, Cultural Encounters in Late Antiquity and the Middle Ages, vol. 12, Turnhout, Brepols.
Waeltner, Ernst L. (1977), Organicum Melos. Zur Musikanschauung des Iohannes Scottus (Eriugena), Munich, Verlag der Bayerischen Akademie der Wissenschaften, https://publikationen.badw.de/en/003316452/pdf/CC%20BY, consulté le 13 septembre 2023.
Wiora, Walter (1971), « Das vermeintliche Zeugnis des Johannes Eriugena für die Anfänge der abendländischen Mehrstimmigkeit. Marius Schneider zum 65. Geburtstag », Acta Musicologica, vol. 43, fasc. 1/2 (janv.-juin), p. 33-43, https://doi.org/10.2307/932499.
Annexe 1 : Originalité de la notion de hauteur, emplois d’altitudo et de profunditas
La hauteur de son
Rappelons que la notion de hauteur de son n’est pas évidente. Elle n’est pas portée par l’opposition acutus/gravis, aigu/grave, qui désigne les deux extrêmes des sons lorsqu’ils sont ordonnés par ordre d’intervalles numériques. Rappelons que la métaphore de l’aigu, acutus, signifie pointu, piquant, ce qui lacère les oreilles ; celle de grave, gravis, signifie lourd, ce qui est émis par des corps pesants. Ces métaphores ne se répondent pas. Elles ne sont même pas unifiées par l’effet produit (pointu/rond ; léger/lourd). Elles désignent en fait des timbres différents selon les lieux où l’on pince la corde et ne s’opposent que par l’entremise visuelle de cordes ordonnées selon les grandeurs mathématiques auxquelles correspond le son. Marie-Élisabeth Duchez (1979) a consacré plusieurs travaux à la question, et a sans doute été la première à pointer les Annotationes de Jean Scot comme le lieu vraisemblable où la hauteur de son est conceptualisée.
Soulignons d’ailleurs que Martianus ajoute que la gravité du son est produite lorsque le souffle est tiré des profondeurs, alors que l’acuité est émise à la surface de la bouche : il ne s’occupe pas d’unifier le corps émettant ces sons en opposant, ce que nous faisons, les résonances de tête et les résonances de poitrine. Au lieu d’une émission continue selon deux pôles opposés, on a ici deux lieux possibles d’émission, les « profondeurs » et la bouche (Capella 2011, § 932, p. 34, et surtout § 939, p. 40). Une technique vocale antique ?
Calcidius utilise l’opposition accentus/succentus pour en parler (Calcidius 2011, I, 44, p. 256 et note 229) : l’idée de hauteur est liée à celle d’accent qui traduit le grec oxus phtongos, c’est-à-dire la métaphore d’un timbre perçant : l’image de la hauteur, comme conceptualisation d’un paramètre, est absente. Acumen est fréquemment employé, y compris pour le son25Par exemple, Calcidius 2011, I, 40, p. 250. Mais c’est un terme très fréquent.. Il s’agit alors de l’idée d’un sommet, ou plutôt du pointu du sommet, et non celle de gravir une montagne continue. D’ailleurs chez lui, les planètes et le Soleil ne « montent » pas, ni ne « descendent » : ce sont les termes d’effulsio (jaillissement), d’obscuratio ou occultatio (assombrissement, occultation), ortus et occasus, (naissance) et « chute » qui sont utilisés26Par exemple, ibid., I, 70-71, p. 289. Ce que Béatrice Bakhouche traduit par « C’est pourquoi ils [Vénus, Mercure, Mars, Jupiter] ne s’accordent pas avec le parcours du Soleil, par leurs périodes d’apparition et de disparition que nous appelons levers et couchers » ou « de la même façon, le coucher, c’est proprement le début de la descente (descensus au-dessous du cercle de l’horizon ; dans un autre sens cependant, c’est aussi le début de la disparition d’une étoile, quand le Soleil l’obscurcit ».. Boèce consacre un passage de son Traité de la musique (De institutione musica) à se demander si la Lune sonne grave ou aigu, c’est-à-dire par où commence la gamme du ciel (Boèce 2004, I, XXVII, p. 85). Mais lorsqu’il explique l’ordonnancement des intervalles, il place le grave en haut (ibid., I, XXIV, p. 81) : en fait, la question n’est pas importante pour lui puisqu’il pense le son en diastemata, ce qui est cohérent avec son écriture de la musique où il utilise autant de lettres alphabétiques qu’il y a de consonance dans chaque genre vocal ou instrumental. La conceptualisation précise de la hauteur de son lui est totalement étrangère. Par exemple, lorsque Christian Meyer, pour plus de clarté, traduit par « monte » ou « descend », Boèce emploie en fait « croître » (en nombre) ou « décroître », ce qui est, visuellement, bien différent, tout en préparant, bien sûr, la conceptualisation mesurée de la notion de hauteur (ibid., IV, 1, p. 224-225)27« Quae gravis est intentione, crescit ad medium, quae vero acuta, remissione decrescit ad medium » devient ainsi « par une tension, un son grave monte vers une zone moyenne, en revanche, un son aigu y redescend par relâchement ». Lorsque Martianus veut dire la même chose, Jean-Baptiste Guillaumin traduit par « [le sens du mot phtongos s’applique] lorsque, si nous envisageons la représentation graphique qui convient, la fonction du son nous apprend à quel degré d’acuité nous devons monter ou à quel degré de gravité nous devons descendre ». Le texte latin donne « ita haec virtus phthongi docet quid vel acuminis exeramus vel leniminis remittamus » (Capella 2011, p. … Continue reading.
Martianus Capella est beaucoup plus subtil. Chez lui, on monte dans le ciel. Philologie, après avoir vomi toute l’érudition terrestre, peut franchir les 126 000 stades vers la Lune et gravir ainsi les sons célestes, et même au-delà du ton de la Lune. À la fin, la pauvre est très fatiguée après avoir gravi l’ensemble des stades formant l’octave et la perfection d’une harmonie complète28Capella 2001, II, 134, 169, 199, notamment p. 94.. Dans ce cas, il s’agit d’une ascension de distance jusqu’au sommet du ciel, en gravissant les orbes successifs : les intervalles musicaux sont d’abord des mesures convertibles en stades, des diastemata donc.
Jean Scot glose de façon très précise les Noces de Philologie et de Mercure en discutant les termes acuto sonitu employés par Martianus dans le premier livre. Au début de ce long récit, la noce se rassemble dans des grottes et paysages. Évoquant la musique mélodieuse qui émane d’un frémissement harmonieux des arbres du bois sacré en lien métaphorique avec la musique céleste, Martianus écrit : « Les cimes culminantes, et tendues à proportion, des arbres élevés retentissaient d’une modalité aiguë (acuto sonitu) alors que tout ce qui frôlait le sol et avoisinait les branchages inclinés vibrait sous l’effet de notes graves et basses (gravitas rauca) » (Capella 2014, I, 11, p. 9). La musique mélodieuse qui émane d’un frémissement harmonieux des arbres du bois sacré en lien avec la musique céleste est une musique qui vient d’en haut. La métaphore de monter dans le ciel jusqu’au Firmament aigu est bien là. Jean-Frédéric Chevalier traduit par « culminantes » le participe ementiora. Il renvoie pour la discussion du lien entre le sommet des arbres et l’aigu ou le grave des cordes tendues au livre ix des Noces qui semble rétablir un ordre haut-aigu/bas-grave peu clair dans ce passage de Noces I (Capella 2011, IX, § 939-940, p. 40-41 et notes p. 179-181). Soulignons toutefois pour notre propos que, dans le livre ix des Noces, là où le traducteur d’aujourd’hui précise « monter » et « descendre », nous avons bien en latin descendere mais on n’a pas son contraire, qui est donné par les verbes exeramus vel leniminis remittamus, c’est-à-dire des termes décrivant l’action de serrer ou desserrer la tension d’une corde. Pour mieux se faire comprendre, Martianus utilise même l’opposition grecque epitasis/anesis, c’est-à-dire tension/relâchement, et en aucun cas la visualisation complète de l’ascension et de la descente.
Ce passage, avec ses ambiguïtés, peut-être avec l’écho entre les livres I et IX des Noces, a certainement donné à penser à Jean Scot. D’ailleurs il en vient à corriger Martianus : « monter » vers le Firmament n’implique nullement, dit-il, « monter » dans le son : c’est le fait de monter géographiquement vers ce qui est haut dans le ciel (et qui s’avère aussi aigu si on suit l’idée ancienne contestée par Jean Scot que la gamme du ciel est orientée de façon continue entre le lourd à partir de la terre vers le strident du firmament)29« On demande pourquoi Martianus dit que le son aigu (acutus) se trouve dans le sommet des arbres, c’est-à-dire dans la musique céleste, comme si l’aigu était dans Saturne et la gravité dans la Lune. Il dit cela parce quelque chose de l’élément terrestre adhère et sonne plus gravement, et qu’en revanche lorsqu’il sonne dans des lieux plus purs, il est plus aigu » (Jeauneau 1978, p. 18-119).. L’Érigène reprend donc Martianus sur sa géographie céleste : il insiste sur le fait que acutus ne fait que désigner une proportion mathématique, mais que Saturne, la plus éloignée, est grave. Donc on peut bien monter vers Saturne comme on monte à un arbre ou dans le ciel, mais dans ce cas on ne monte pas vers l’aigu mais vers le grave. Il est impossible de monter de façon régulière jusqu’au Firmament tout en montant dans l’aigu. Jean Scot précise donc très fermement que Martianus utilise le mot tonus pour parler de distance avec une mesure fixe, alors qu’en fait il faut comprendre tonus comme une mesure du son30Voir les explications très détaillées de Teeuwen 2002, p. 228..
Jean Scot peut alors corriger Martianus en construisant une véritable échelle sonore autonome et non pas simplement un ordonnancement d’intervalle mesurés : il réinterprète le texte en lui appliquant une échelle de sons indépendamment des lieux géographiques du cosmos. C’est en fait une reformulation complète de ce que dit Martianus. Dans cette glose sur « Acuto sonitu » on assiste peut-être aussi, en même temps qu’à la naissance de la conceptualisation de la hauteur, à l’idée d’échelle sonore, qui fera l’objet d’un travail serré de la part de la Scolica enchiriadis.
Arpad Szabo émet l’hypothèse que c’est Aristoxène qui aurait soulevé la question haut/bas pour le son. Dans sa démarche de se libérer de l’emprise du nombre sur le monde, il aurait mis en évidence la contradiction entre le nombre élevé ou faible lié au son et la longueur de la corde attachée à ce nombre (Szabo 1977, p. 183).
Altitudo
L’altitudo est le caractère de ce qui est altus. Il signifie le plus souvent « profond » : dans notre vocabulaire encore, la « haute mer » est la mer profonde. Dans le petit traité de Jean Scot, il y a clairement l’image des planètes qui montent et descendent dans le ciel. Le Soleil et la Lune changent de couleur pro rationibus altitudinum seu descensionum, du fait de leur altitude ou de leur descente (Lutz 1939, p. 11, 23). Nous avons vu également les planètes le faire lorsqu’elles étaient au-dessus ou au-dessous de l’orbe du Soleil, entrant ainsi dans des consonances variées avec lui. De ce fait, en termes de lieux, on monte et on descend, de façon continue. La notion d’altitudo est ainsi liée à un mouvement continu que l’on peut suivre visuellement et qui devient celui des sons dans l’expression altitudo sonorum puisque les planètes sont liées au son de la clameur divine.
Calcidius utilise trois termes. Il emploie d’abord le mot crassitudo, c’est-à-dire densité, solidité, pour la nature des corps du monde, opposée à ceux qui n’auraient que deux dimensions : « si le corps de l’univers devait posséder seulement une longueur (longitudo) et une largeur (latitudo) mais pas d’épaisseur (crassitudo) » (Calcidius 2011, 32A, p. 161). Le commentaire reprend ce mot (ibid., I, 8, p. 211). Il emploie également, pour les corps solides, le mot de profunditas, dans le contexte de leur nature géométrique, en les opposant au point et à la ligne :
Ce qui n’a pas de partie et qui, pour cette raison, ne tombe pas sous les sens, mais qui existe et qui est perçu par l’âme, les géomètres l’appellent point, tandis qu’ils appellent ligne une longueur sans largeur et qui a des extrémités ; ce qui comporte une largeur il l’appellent surface si bien que la surface c’est une longueur (longitudo) avec une largeur (latitudo) et ce qui est composé de trois dimensions, c’est-à-dire d’une longueur, d’une largeur et d’une profondeur (profunditas), ils le dénomment corps solide. (Ibid., I, 32, p. 241)31Voir encore I, 118, p. 353 ; ou I, 121, p. 359 : les sept mouvements de l’espace, deux en longueur vers l’avant et vers l’arrière, deux en largeur vers la droite et vers la gauche, deux en hauteur, vers le dessus ou le dessous : profunditas, sursum, deorsum, et le dernier autour d’un axe fixe, c’est-à-dire la rotation. Béatrice Bakhouche remarque (note 10 p. 723) qu’Aristote comme Martianus refusent la rotation à l’homme. Une étoile pour Calcidius n’a que deux de ces sept mouvements alors que Jean Scot, sans le dire clairement, les possibilités semblent plus ouvertes.
Calcidius emploie profunditas et non pas altitudo pour la troisième dimension d’un corps.
On trouve les trois mots dans le contexte du calcul effectif sur les objets à trois dimensions. Altitudo est lié à celui de soliditatem dans le contexte du calcul applicable à des objets à trois dimensions, mais ramené à des surfaces : la hauteur du triangle est altitudo (ibid., I, 12, p. 215). Elle permet de comprendre le corps de l’univers qui possède une épaisseur, soliditatem (ibid., I, 13, p. 217), ici, donc, synonyme de crassitudo. Le corps du monde est solide et sphérique, solidus et globosus. Mais lorsqu’on se met à faire le calcul effectif, le corps du monde, sphérique, est donc relié par deux médiétés (puisqu’il a trois dimensions, il faut deux médiétés pour relier ces trois dimensions à l’opposition de deux contraires, le même et l’autre). Il y a une médiété qui dépend de la surface, donc de la longueur, longitudo, et une autre de la largeur, latitudo. Il y en a aussi une autre qui dépend de la profondeur, profunditas, « médiété où aboutit ce point si on l’enfonce jusqu’au milieu de la hauteur », altitudo (ibid., I, 13, p. 219). Il y a donc une opposition ferme entre profunditas, ou crassitudo ou soliditas, termes synonymes qui désignent la troisième dimension dans la dimension solide des objets, y compris la matière ignée, et altitudo, terme utilisé pour désigner la hauteur d’un triangle, et donc pour mesurer la hauteur d’un objet de trois dimensions, rapportée à de la géométrie de l’espace.
C’est pourquoi on retrouve le mot altitudo dans le contexte astronomique. Calcidius l’utilise très précisément pour désigner les distances des astres errants : « Comment on trouve, pour les astres errants, leur distance moyenne et leur distance minimale (quatenus accidat maxima stellarum errantium altitudo, quae media, quae minima), qu’ils se déplacent soit sur des cercles excentriques, ou sur des épicycles » (Calcidius 2011, i, 87, p. 315). Chez Calcidius, la position médiane (entre apogée et périgée) est appelée altitudo media. C’est là que se trouvent, pour Jean Scot, les consonances.
Le mot est travaillé de façon générale dans le Periphyseon, dans le cadre d’une réflexion générale sur ce qu’est un corps. Un corps a forcément trois dimensions sinon il est incorporel (Periphyseon I, 491B, Scot Érigène 1995) :
Toute quantité s’étend sur trois dimensions, longueur, largeur, hauteur (in tribus spatiis extenditur, longitudine quidem, latitudine, altitudine), et ces trois dimensions (spatia) s’étendent à leur tour en six directions (trio spatia senario protenduntur numero). Car la longueur s’étend vers le haut et vers le bas (sursum et deorsum), la largeur vers la droite et vers la gauche (dextrorsum et sinistrorsum), la profondeur vers l’avant et vers l’arrière (ante et retro). (Periphyseon I, 464B, ibid.)
Comment traduire retro et ante, c’est-à-dire littéralement « avant » et « arrière » pour l’altitude où l’on attendrait plutôt « en bas » et « en haut » ? Francis Bertin, le traducteur français du Periphyseon a préféré le terme de « profondeur » pour altitudo, afin de conserver la cohérence de cette analyse générale. Or Scot n’utilise pas le mot de crassitudo qui est celui de Calcidius.
En fait, cette difficulté n’en est pas une si l’on comprend que pour le cosmos on regarde la surface d’une sphère (qu’il s’agisse de la planète ou de son orbite) de l’intérieur : alors la longueur est bien de haut en bas et la largeur de gauche à droite. De ce point d’observation il y a aussi la profondeur, devant et en revenant vers soi. La confirmation du sens cosmologique, relationnel, géométrique d’altitudo se trouve dans les gloses sur Martianus, parce que le mot y est alors lié au cas précis des planètes et de la mesure de leurs orbes respectives. D’abord, dans l’espace, rappelle fermement Jean Scot, « le haut et le bas ne conviennent pas » (Jeauneau 1978, p. 124). Par ailleurs, altitudo désigne un lieu qui est un rapport de rapport.
D’autres passages des gloses semblent aller dans ce sens : la notion d’altitude est utilisée pour rendre compte des consonances variables qui surviennent entre planètes selon leur parcours :
Ainsi tu le vois ces mêmes intervalles [des différentes conjonctions entre le Soleil et Saturne] ne s’approchent pas toujours d’un son si ce n’est selon l’altitude des abscisses (altitudo absidarum), ce qui donc est admirable si, lorsque le Soleil forme avec Saturne un accord de diapason doublé alors il en est écarté dans sa course à sa plus longue distance, mais lorsqu’il s’approche, il forme une quinte en proportion 3 à 2 et lorsqu’il est très proche, il sonne une quarte en proportion 4 à 3. (Ibid., p. 125)
On peut alors concevoir la conjonction entre les points des différents orbes, que l’on peut mesurer : c’est à quoi sert la consonance c’est-à-dire le son qui existe à un moment donné, lorsqu’il y a rencontre consonante avec l’altitude d’une autre planète, quelle que soit leur ordonnance géographique dans le cosmos. Il ne s’agit plus de chercher à mesurer des intervalles ou distances entre sphères emboîtées les unes dans les autres mais les rencontres harmoniques que chaque planète produit avec les autres, dans tous les mouvements des différentes orbites, d’autant qu’il y a deux centres pour ces sphères emboîtées, la Terre et le Soleil. L’altitude devient le concept qui permet de rendre compte de la consonance propre à l’intervalle de chaque planète en rapport avec les autres32Lorsqu’elle le rencontre chez Jean Scot, Erika von Erhardt-Siebold est déconcertée par le mot (Erhardt-Siebold et Erhardt 1940, p. 13) : elle relève par exemple que Jean Scot dit « pro rationibus altitudinum seu descensionum » (Annotationes 11, 23). Toutefois, remarque-t-elle, « d’abord nous ne savons pas ce qu’il entend ici par altitudo et descensio, puisque l’Annotateur, comme Capella, utilise sans distinguer les mouvements de latitude de ceux qui concernent les profondeurs de l’espace ». Elle relève des occurrences qui vont dans le même sens, mais pourtant, dans ces relevés, on ne trouve pas le mot précis d’altitudo (Annotationes 433, 12, glose de … Continue reading.
Il semble donc que l’altitude des sons soit le fait de se rapporter à une intersection de mouvements circulaires en trois dimensions. On n’est plus dans une mesure linéaire. Le mot « altitude » est donc celui qui convient pour désigner les caractéristiques du son cosmique, seule manière de mesurer ce qui échappe à la mesure. Ainsi l’altitudo, la hauteur des sons spatiaux, variable selon les conjonctions des astres, est nettement différenciée des distances ordonnées entre orbites dans le ciel. Elle est déterminée par la consonance générée avec les autres dans les trois dimensions propres au volume de chaque orbe.
La notion de hauteur de son est systématiquement pratiquée par Jean Scot. Percy Jones remarque que partout, il commence par le bas et monte. La paranète est pour lui la troisième note du tétracorde et non pas la seconde (Jones 1957, p. 108). Surtout, en regardant de près les Annotationes, on se rend compte qu’il la théorise, en lien avec la pratique musicale.
Soulignons enfin que altitudo est l’une des caractéristiques du nombre : il y a des nombres linéaires, des nombres plans et des nombres solides, que l’on peut disposer selon trois dimensions. Ainsi les pyramides, les cubes, les sphères (Isidore 2009, p. 32 ; Boèce 2002, p. 107). Altitudo est donné comme strict synonyme de crassitudo et profunditas (Boèce 2002, p. 107). Cette façon d’aborder les nombres en mathématiques a sans doute favorisé le passage entre l’idée d’une « hauteur » numérique et celle d’une « hauteur » sonore : il s’agit d’abord de nombres, comme le répète Jean Scot.
Annexe 2 : Proposition de traduction française du traité musical De armonia caelestium motuum siderumque sonis de Jean Scot dit l’Érigène
Le texte est édité par Édouard Jeauneau (Jeauneau 1978, p. 123-132). John MacInnis en a proposé une traduction anglaise (MacInnis 2014, p. 115-129) et Ilaria Ramelli une traduction italienne (Scot Érigène 2006, p. 789-791). Nous nous limitons ici à ce mini-traité.
Sur l’harmonie des mouvements célestes et les sons des astres
Il y a huit sons, à savoir sept sons des planètes et un de la sphère [des fixes]. Parmi eux, le son le plus grave est celui de Saturne, mais le plus le plus aigu est le sphérique. En conséquence, le son de la sphère consonne avec le son de Saturne dans un rapport quadruple [2 x 2/1] et l’ensemble atteint un double diapason [deux octaves], comme, pour l’orgue ou la lyre, le rapport entre la principale des principales et l’ultime des excellentes. Mais le son du Soleil est situé entre Saturne et la sphère, comme la µέση [mèse] se trouve entre les deux cordes déjà mentionnées : en effet, il est au-dessus (superat) de Saturne et consonne avec lui par un diapason de rapport double [2/1, octave], mais il est moins haut (superatur) que la sphère par un rapport double [2/1] et il compose avec elle un autre diapason [octave]. Où l’on doit admirer la puissance admirable de la nature. En effet, ce qui est construit par les cinq tétracordes [c’est-à-dire les deux octaves] est accompli par les huit sons célestes. Mais quelle rationalité y est à l’œuvre, c’est ce qu’il faut à présent examiner par une recherche attentive et diligente.
D’abord donc, comprends que les trois planètes qui sont situées dans les lieux surplombant le Soleil ont des sons plus graves. Ce n’est pas sans raison, parce qu’elles rencontrent de la gêne, à la fois parce qu’elles se meuvent dans des espaces du monde plus grands et du fait de la très grande vitesse sphérique face à laquelle elles suivent une course contraire, de sorte que leur vitesse est moins grande. De plus, celles qui sont localement sous le Soleil, à la fois parce qu’elles sont à une plus grande distance de la rapidité sphérique et que leur course se produit dans des espaces du monde plus petits, déploient des sons plus aigus. Et conformément à cela, ce n’est pas la position des lieux [des planètes] mais le rapport des proportions des sons qui constitue l’harmonie céleste, d’autant plus que, en ce qui concerne les lieux dans l’univers, ce rapport ne correspond pas au haut et au bas (sursum et deorsum). C’est par la qualité au contraire que le caractère grave, aigu ou médian des sons produit des symphonies qui se répondent diversement.
Prenons le genre diatonique pour exemple. Le Soleil donne un diapason [octave] par un rapport double avec Saturne, et de même, la sphère donne un autre diapason [octave] avec le Soleil ; et par là, la sphère consonne avec Saturne dans un quadruple rapport de deux diapasons [octave, 2 x 2/1]. Et il faut noter que tout diapason [octave] est constitué de huit sons, sept espaces, six tons. Saturne est donc la première dans les plus graves, reliée à Jupiter, la plus proche, par un ton ; Jupiter de même [est liée à] Mars par un ton ; le Soleil à Mars par un demi-ton et entre le Soleil et Saturne se trouve un diatessaron [quarte] en proportion sesquitierce [4/3]. Avec les mêmes sons, le Soleil entre en consonance avec Saturne par une symphonie de sesquialtère [3/2, quinte] de la manière suivante : entre Saturne et Jupiter, un ton, entre Jupiter et Mars, un ton, entre Mars et le Soleil, un ton, et tu as à la fois un diapente [quinte] et un diatessaron [quarte] entre le Soleil et Saturne33Aucun commentateur n’a, à notre connaissance, expliqué l’étrangeté de cette quinte faite de trois tons entiers, d’autant qu’au-dessous du Soleil, la quinte supérieure est ensuite clairement détaillée, en ajoutant un cinquième son, celui des Fixes. La phrase suivante invite à penser que Saturne peut être très éloigné et qu’alors peut-être il faut ajouter le demi-ton qui manque.. Et tu ne t’étonneras pas que le Soleil entre en concordance avec les autres planètes dans de multiples proportions. Nous avons dit, en effet, qu’il est en consonance de trois façons avec Saturne, à savoir par une conjonction double, sesquitierce et sesquialtère [octave, quarte et quinte ; 2/1, 4/3, 3/2]. Si tu considères qu’ils ne s’approchent pas toujours par les mêmes intervalles de son mais selon la hauteur [altitude] (altitudo) de leurs absides, qu’y a-t-il donc d’étonnant [à comprendre que] le Soleil est en consonance avec Saturne par un diapason en rapport double [2/1], lorsqu’il [le Soleil] parcourt les trajets éloignés d’elle [Saturne] dans les plus grandes distances ? mais lorsqu’il commence à se rapprocher d’elle, elle fera sonner un diapente [quinte] en proportion sesquialtère [3/2] ; et s’il s’approche au plus près, sonnera un diatessaron [quarte] en sesquitierce [4/3].
Une fois considéré ce rapport, tu ne t’étonneras pas, je pense, que nous disions aussi de Mars qu’elle est séparée du Soleil parfois par un ton et parfois par un demi-ton. En effet, ce qui vaut pour les cordes, le fait qu’elles soient tendues ou détendues, qu’elles soient longues ou courtes vaut de la même façon pour les tuyaux d’orgue dont la taille détermine le ton34Nous lisons spatia faciunt ou bien spatium facit. ; il en va de même en ce qui concerne les planètes, avec la hauteur [altitude] (altitudo) de leurs absides et leur éloignement ou leur proximité du Soleil. Et ce que nous avons dit du Soleil, il faut comprendre qu’il en est de même, mutuellement, pour toutes les planètes. En effet, ce n’est pas toujours par les mêmes intervalles que soit, alternativement, elles prennent de la distance, soit, inversement, elles se rapprochent, en raison de la situation de leurs absides ; et il faut croire ainsi que toutes les consonances musicales peuvent être obtenues par les huit sons célestes, non seulement dans les trois genres, diatonique, chromatique et enharmonique, mais aussi dans d’autres qui se situent au-delà de la capacité de calcul de tous les mortels. Mais on peut trouver un diapason [octave] de cette façon : au-dessus du Soleil [pour] la hauteur des sons aigus (altitudo acuminum), et en revanche au-dessous du Soleil [si l’on considère] la position [géographique] des lieux telle qu’elle apparaît aux sens des mortels. Le Soleil est relié à la sphère par un diapason, et il a d’abord un diatessaron [quarte] avec la Lune, et avant elle il consonne d’un ton avec Vénus. Mercure consonne d’un autre ton avec Vénus, la Lune d’un demi-ton avec Mercure. Mais la consonance de diapente [quinte] [a lieu] dans les mêmes espaces, lorsque Vénus répond d’un ton avec le Soleil, Mercure d’un ton avec Vénus, la Lune d’un demi-ton avec Mercure, et la sphère d’un ton avec la Lune.
Et il faut noter que ceux des tons qui sont comptés de la terre à la sphère, par exemple le ton de la terre à la Lune, ne sont pas des proportions de voix [de sons déterminés], mais des intervalles de lieux. Il existe en effet plusieurs espèces de tons. Lorsque les tons sont les intervalles [qui séparent] des astres, c’est-à-dire s’il s’agit de savoir de combien l’un est distant de l’autre et de combien la Lune est éloignée de la terre, ces tons varient selon la diversité des absides et des cercles [la diversité des orbites et des trajectoires visibles]. C’est cette espèce de ton que Martianus définit en disant : « le ton est un espace doué d’une grandeur bien définie35Capella 2011, § 930, p. 30. Jean-Baptiste Guillaumin traduit par « un intervalle d’une grandeur bien définie » et insiste, dans son apparat critique, sur la polysémie du terme tonus. ». Cette espèce est appelée diastema en musique. Il y a des tons pour les temps, constitués en longueur et brièveté. Il y a des tons de souffle, définis par la densité et la gracilité de la voix36Ilaria Ramelli traduit spiritus par intensità ; spisitudo et exilitas vocum par robustezza et delicatezza di voici. John MacInnis traduit spiritus par breath ; spisitudo et exilitas vocum par density ou sparseness of sounds. S’agirait-il d’une allusion à ce que notent les neumes ?. Il y a des tons harmoniques, dont il s’agit à présent, en gravité et hauteur des sons (altitudo sonorum), à partir desquels est constituée toute la proportionnalité des symphonies. C’est pourquoi, de même que pour l’orgue on ne considère pas le lieu où se trouve le tuyau mais quelle est sa voix [son déterminé] et à combien [d’autres tuyaux] et avec lesquels il est relié et quelles proportions il produit ‒ chaque tuyau combiné avec beaucoup d’autres donne des symphonies diverses ‒, de même ce n’est pas le lieu des astres mais leur son qui compose l’harmonie céleste. Il est vrai que les voix [les sons déterminés] des astres évoluent selon les espaces séparant les absides, et ce n’est pas étonnant puisque nous voyons à la fois que, pour la même raison, leurs couleurs changent et qu’une corde placée dans un espace plus court ou plus grand, soit tendue, soit relâchée, ne rend pas la même voix [le même son déterminé]. bien qu’elle soit la même [bien qu’elle ne change pas de nature].
Le mot « ton » (tonus) de plus provient de « tendre » (tendendo) ; il est grec et dérive du verbe τείνω [teino], c’est-à-dire « j’étire ». Mais ce qui est proprement signifié par « octaves » relève de l’usage des musiciens, parce que [l’octave] est la mesure commune de toutes les proportions. Et ne t’étonne pas que nous ayons parlé d’un ton entre la Lune et le Soleil. Ici, en effet, nous ne considérons pas les tons de lieux, c’est-à-dire les espaces, mais les consonances des voix [sons déterminés]. En effet, lorsque nous commençons rationnellement par le plus grave de tous les sons, à savoir Saturne, et que, par une ascension proportionnelle, nous montons jusqu’à la médiété du son solaire, et de là, étendant le rapport dans la partie supérieure (superius), nous parvenons au son le plus aigu de toutes les planètes, celui de la Lune ‒ ce qui est justifié car cette dernière occupe la plus étroite de toutes les zones de passage –, là où nous ne pouvons pas monter plus haut (altius ascendere), le rapport nous a amenés au mouvement de la sphère céleste, le plus aigu de tous les sons, et de la sorte nous avons joint le plus aigu de tous les sons planétaires au son le plus aigu et le plus éloigné du mouvement du monde entier, par le [seul] rapport du ton.
Ainsi, la cause de beaucoup d’erreurs vient de l’ignorance des tons, chez ceux qui croient que le ton par lequel la Lune est distante de la terre est pertinent pour [parler des] proportions des voix [de sons déterminés] célestes, alors qu’ils ne se rendent pas compte auparavant qu’un ton musical est constitué de deux sons, et que la terre, parce qu’elle est immobile, ne produit aucun son. Il n’y a donc pas de ton musical entre la terre et la Lune. Il en résulte que jamais les intervalles musicaux ne sont mesurés en nombre de stades, mais par la seule ascension calculée de l’extension, selon les règles des nombres37Expression apparemment obscure, mais qui décrit la manière d’obtenir et de comparer des rapports, des proportions, le fait qu’un même logos relie les termes entre eux, c’est-à-dire ce qui concerne les intervalles musicaux. Par exemple, dans le sens de la croissance et de l’extension, on passe de 1 à 2 (rapport double, d’octave) en ajoutant l’unité à l’unité ; puis de 2 à 3 (rapport sesquialtère, de quinte) en ajoutant la moitié de 2 à 2 ; puis on passe de 3 à 4 (rapport sesquitierce de quarte) en ajoutant un tiers de 3 à 3, etc. Les rapports diminuent, mais les nombres croissent, c’est une « ascension calculée », et ils s’étendent de sorte à rendre … Continue reading. C’est une chose, en effet, que de mesurer 126 000 stades entre la terre et la Lune, et une autre chose que de mesurer la différence entre le nombre 192 et 216, soit 24 unités. Là, le ton est de 126 [mille] stades ; ici, le ton est de 24, la huitième partie du plus petit nombre.
Utilisons donc un exemple pour qu’apparaisse de façon plus manifeste ce que nous cherchons à établir. Dans un chœur, où beaucoup de chanteurs produisent ensemble des consonances, on ne considère pas le lieu où chacun se trouve mais la proportion de sa voix [avec celle des autres]. En effet, quel que soit le lieu où se trouve celui qui émet le son le plus grave, il est nécessaire que la plus grave de toutes les voix produise la bonne proportion. Par la même raison, où qu’il se trouve dans le chœur, celui qui émet la voix [son déterminé] la plus aigüe tiendra nécessairement le sommet de tous les sons. Il faut comprendre de la même façon que, dans ce qui suit, on ne juge pas la position locale mais l’émission vocale proportionnelle dans l’ensemble des modulations. C’est donc en vain qu’on pensera rendre la musique céleste par une proportion d’intervalles liés aux lieux. En ceci, nous n’examinons rien d’autre que la montée et la descente à propos du caractère grave ou élevé du son (gravitatis et acuminis ascensus atque descensus). De même en effet qu’un son grave monte en hauteur (in altitudinem) en diminuant jusqu’à ce qu’il atteigne la limite la plus aiguë, de même et de façon semblable, la hauteur [d’un son] descend, en augmentant38Nous lisons, comme MacInnis (2014, p. 125) crescendo au lieu de decrescendo. Mais notre traduction demeure générale et ne se réfère pas aussi explicitement que la sienne à la longueur d’une corde vibrante, dans la mesure où nous sommes bien ici dans des proportions qui augmentent ou diminuent et non pas dans des distances, même si la corde tendue est clairement le modèle de pensée (le paragraphe précédent parle bien d’extensio mais ajoute « selon la règle des nombres » [secundum regulas numerorum]). progressivement jusqu’à ce qu’elle trouve son point ultime dans le grave.
[Voici la doctrine de] la secte platonicienne des Grecs les plus anciens au sujet de la chute et de l’apostrophia39Retour, en grec et en caractères romains dans le texte. des âmes. Comme toutes les âmes créées en même temps avant les corps terrestres sont dévoyées dans les accès célestes aux étoiles, et que, ne pouvant ou ne voulant pas atteindre la vitesse de la sphère céleste, mais choisissant la lenteur de Saturne, elles glissent d’abord de leurs habitations célestes dans le pourtour de Saturne ; puis, commençant à tomber, sans raison suffisamment forte pour les retenir, elles sont obligées de tomber à travers les différents cercles [trajectoires visibles] des planètes jusqu’aux corps terrestres, dont, souillées par les diverses saletés de leurs péchés, elles doivent à nouveau se séparer et descendre dans les enfers, c’est-à-dire vers cette vie qui suit la mort de la chair. Et parce qu’ils [les Grecs les plus anciens] pensaient qu’il n’y a rien en dehors du monde, ces zones de passage des planètes par lesquelles ils imaginaient que les âmes glissent dans les corps, ils pensaient que ces mêmes âmes y retournaient, retrouvant ainsi leur premier emplacement comme de nature. Mais souillées de taches corporelles, sans le nettoyage qu’ils appelaient ἀποθέωσις [apotheosis, apothéose] c’est-à-dire nouvelle déification, (puisque, comme ils le pensaient, elles [les âmes] adhéraient d’abord à l’unité divine vers laquelle elles retournaient une fois nettoyées), elles ne pouvaient pas y parvenir [à retourner à l’unité divine] ; pour cette raison, ils estimaient que [les âmes] étaient nettoyées dans ces zones de passage des planètes ; et parce que les espaces éthérés n’ont pas la même qualité, – on dit en effet que certains sont froids, mais d’autres ardents et d’autres tempérés –, ils pensaient que les qualités propres devaient être appréciées au cas par cas. Et ils appelaient Styx, c’est-à-dire tristesse, la zone de passage de Saturne : c’est à cela que Martianus fait allusion lorsqu’il parle de Saturne comme « le plus triste des dieux », du fait de son très grand froid qui provient de son éloignement du Soleil et de la lenteur de sa course. Mais la zone de passage de Mars, ils l’appelaient πυρφληγέτον (sic) [pyriphlegéthôn], c’est-à-dire feu flambant. Dans ces deux zones de passage, ils [les Grecs] pensaient que les âmes impies sont soit torturées éternellement si elles sont d’une méchanceté excessive, soit nettoyées de sorte à pouvoir retrouver un genre de repos. Cette tranquillité, ils pensaient qu’elle se trouve dans la zone de passage située entre Jupiter et Vénus, où ils pensaient que sont les champs ελυσεος (sic) [elyseos], c’est-à-dire de dissolution des peines. Mais parce que, ni dans le nettoyage ni dans le repos, elles ne peuvent oublier l’amour des corps auxquels elles sont unies à la naissance, certaines, même nettoyées, souhaitent à nouveau retourner vers les corps, tandis que d’autres, méprisant complètement les corps, vont naturellement vers leurs étoiles, évidemment celles d’où elles sont tombées. C’est pourquoi il [Martianus] dit que certaines [âmes] s’en retournent aux rivages, c’est-à-dire à leur état premier, mais que d’autres sont totalement libérées des corps. Et le libre examen des âmes, par lequel ils [les anciens Grecs] se demandent si elles sont renvoyées vers les corps ou si, ayant méprisé toute habitation corporelle, elles sont renvoyées vers leurs demeures antérieures, c’est ce qu’il [Martianus] désigne par « le retour », allant de courant en courant du fait d’une autre fortune et refluant de fleuve en fleuve40Nous lisons fortunarum, un mot que l’on retrouve chez Capella (2001, I, 11, 14, 15, p. 9, p. 11, p. 12, etc.).. L’onde livide41Ibid., I, 14, p. 10., comme il le dit lui-même, n’a pas pu les retenir. La liberté de l’âme humaine est telle que, si elle veut demeurer dans la misère, elle y demeure, mais si [elle tient à] son intégrité, elle la conserve. En voilà assez de la misère des pensées humaines et des machinations intellectuelles dénuées de foi.
| RMO_vol.10.2_Anger |
Attention : le logiciel Aperçu (preview) ne permet pas la lecture des fichiers sonores intégrés dans les fichiers pdf.
Citation
- Référence papier (pdf)
Violaine Anger, « Altitudo sonorum. La conceptualisation de la hauteur de son dans les gloses sur Martianus Capella de Jean Scot, dit l’Érigène », Revue musicale OICRM, vol. 10, no 2, 2023, p. 99-130.
- Référence électronique
Violaine Anger, « Altitudo sonorum. La conceptualisation de la hauteur de son dans les gloses sur Martianus Capella de Jean Scot, dit l’Érigène », Revue musicale OICRM, vol. 10, no 2, 2023, mis en ligne le 27 novembre 2023, https://revuemusicaleoicrm.org/rmo-vol10-n2/altitudo-sonorum/, consulté le…
Autrice
Violaine Anger, Université d’Évry/École polytechnique (Paris)
Ancienne élève de l’École normale supérieure et du Conservatoire national supérieur de musique de Paris, habilitée à diriger des recherches, Violaine Anger enseigne à l’Université d’Évry et à l’École polytechnique (Paris). Membre du Centre d’étude de l’écriture et de l’image (CEEI, Paris), elle poursuit sa recherche au Centre d’études et de recherches comparées sur la création (CERCC, Lyon), Équipe d’accueil 1633. Elle a écrit Tchaïkovski (J.-P. Gisserot, 1998), Le sens de la musique, vol. 1 et 2 (Éditions Rue d’Ulm, 2005), Sonate, que me veux-tu ? (ENS Éditions, 2016), Berlioz et la scène. Penser l’incarnation théâtrale (Vrin, 2016), Giacomo Meyerbeer (Bleu Nuit, 2017), Voir le son. L’écriture, l’image et le chant (Delatour, 2020), Victor Hugo et la mélodie française (Paris, Hermann, 2023), ainsi que de nombreux articles.
Notes
| ↵1 | L’utilisation du genre masculin a été adoptée afin de faciliter la lecture et n’a aucune intention discriminatoire. |
|---|---|
| ↵2 | Il s’agit d’un texte pédagogique qui raconte les noces du dieu Mercure avec la mortelle Philologie et l’ascension de cette dernière vers l’apothéose, à l’aide des arts libéraux : par le savoir, de moins en moins liée à la pesanteur et à l’irrationalité terrestres, elle devient immortelle. |
| ↵3 | Voir annexe 2 pour une proposition de traduction. |
| ↵4 | Texte de Capella : « Constat autem omnis modulatio ex gravitate soni vel acumine ». Glosé : « acumen : altitudo ». |
| ↵5 | « Altitudo est quando circulus alicuius planetae altius elevatur a terra ». Jean Scot glose Martianus, Astronomie VIII, 884, qui donne lui-même déjà une définition très proche : « eius altitudo, id est ubi se eius circulus a terra altius tollit ». Scot insiste sur le mouvement là où Martianus ne voit que le cercle. |
| ↵6 | « Sunt toni armonici, de quibus nunc agitur, in grauitate et altitudine sonorum ». |
| ↵7 | Notre traduction, comme toutes les citations à venir de ce texte édité par Jeauneau. |
| ↵8 | Teeuwen (2002, p. 333-335) a relevé cette mention incontestable de la polyphonie vocale dans le texte du maître irlandais. |
| ↵9 | « In proportionibus vocum, sed in intervallis locorum ». |
| ↵10 | « Non enim locorum tonos, hoc est spatia, hic consideramus, sed vocum consonantias ». |
| ↵11 | « Non locorum positio sed proportionibus sonorum ratio caelestem efficit ». |
| ↵12 | « Frustra igitur localium intervallorum rationibus caelestem musicam coartari arbitrantur ». |
| ↵13 | « Quemadmodum in organo non consideratur in quo loco sit fistula, sed qualis vox ipsius est ». |
| ↵14 | « Non localis positio sed proportionalis vociferatio in universitate modulaminis ». |
| ↵15 | « In his omnibus non locorum positio sed vocum proportio consideratur ». |
| ↵16 | Jean-Baptiste Guillaumin traduit plus précisément par « un intervalle d’une grandeur bien définie » et insiste, dans son apparat critique, sur la polysémie du terme tonus. |
| ↵17 | « Intervallum vero est non silentii inter ptongos, sed spacii » : « l’intervalle entre les ptongues n’est pas de silence mais d’espace » (Scolica enchiriadis III, Gerbert et Schmid 1981, p. 124 ; notre traduction). |
| ↵18 | « Le genre diastématique doit être rattaché à la partie de la musique que l’on nomme l’harmonique » (Capella 2011, 937, p. 39). Voir annexe 1 sur le vocabulaire autour de la notion de hauteur de son. |
| ↵19 | Voir à ce sujet Freyburger 1996, p. 283-292. Ces mesures ont été sévèrement critiquées par Pierre Duhem qui voit chez Jean Scot un prédécesseur de l’astronome Tycho Brahe (avec l’idée que quatre planètes tournent autour du Soleil), mais qui néglige son système de pensée (Duhem 1913-1959, III, p. 62). |
| ↵20 | Le Pamphylien Er raconte un voyage que nous pourrions appeler « chamanique » dans le cosmos. Il y a vu en particulier les planètes tourner autour du fuseau de la nécessité, avec, assise sur chaque planète, une sirène qui émet un son. |
| ↵21 | Voir annexe 1 sur altitudo. |
| ↵22 | Ce que dira explicitement la Scolica enchiriadis (troisième partie). |
| ↵23 | Cette diatribe se retrouve aussi dans les Annotationes, 13, 1, Lutz 1939, glose de « Hi igitur cursu ». |
| ↵24 | Jean Scot semble avoir été professeur d’Heiric d’Auxerre, lui-même professeur de Rémi d’Auxerre et de Hucbald de Saint-Amand, auteur du De Musica où l’on trouve pour la première fois l’écriture sur ligne. Voir à ce propos Jones 1957, p. 86 et 95, qui lui-même s’appuie sur les citations transcrites par Kenney 1929, tome 1, p. 592. Jean Scot a été aussi professeur de Martin de Laon, dont les gloses sont beaucoup moins importantes (Jones 1957, p. 102). Percy Jones ne trouve aucun lien entre les gloses sur Martianus de Jean Scot et les textes de la même famille (rattachés à l’Enchiriadis) à part l’analyse typologique d’Orphée et Eurydice, alors qu’il en trouve beaucoup chez Rémi d’Auxerre (ibid., p. 92). Yves Chartier fait toutefois observer que l’on retrouve la même analyse des six consonances classiques et croit sentir « un enseignement commun à celui d’Hucbald » entre la Scolica enchiriadis, la Musica de Guillaume d’Hirsau et celui, chronologiquement antérieur, de Jean Scot (Chartier 1995, p. 243, § 13). |
| ↵25 | Par exemple, Calcidius 2011, I, 40, p. 250. Mais c’est un terme très fréquent. |
| ↵26 | Par exemple, ibid., I, 70-71, p. 289. Ce que Béatrice Bakhouche traduit par « C’est pourquoi ils [Vénus, Mercure, Mars, Jupiter] ne s’accordent pas avec le parcours du Soleil, par leurs périodes d’apparition et de disparition que nous appelons levers et couchers » ou « de la même façon, le coucher, c’est proprement le début de la descente (descensus au-dessous du cercle de l’horizon ; dans un autre sens cependant, c’est aussi le début de la disparition d’une étoile, quand le Soleil l’obscurcit ». |
| ↵27 | « Quae gravis est intentione, crescit ad medium, quae vero acuta, remissione decrescit ad medium » devient ainsi « par une tension, un son grave monte vers une zone moyenne, en revanche, un son aigu y redescend par relâchement ». Lorsque Martianus veut dire la même chose, Jean-Baptiste Guillaumin traduit par « [le sens du mot phtongos s’applique] lorsque, si nous envisageons la représentation graphique qui convient, la fonction du son nous apprend à quel degré d’acuité nous devons monter ou à quel degré de gravité nous devons descendre ». Le texte latin donne « ita haec virtus phthongi docet quid vel acuminis exeramus vel leniminis remittamus » (Capella 2011, p. 40), alors même que nous sommes, dans le contexte très favorable, d’une représentation graphique. |
| ↵28 | Capella 2001, II, 134, 169, 199, notamment p. 94. |
| ↵29 | « On demande pourquoi Martianus dit que le son aigu (acutus) se trouve dans le sommet des arbres, c’est-à-dire dans la musique céleste, comme si l’aigu était dans Saturne et la gravité dans la Lune. Il dit cela parce quelque chose de l’élément terrestre adhère et sonne plus gravement, et qu’en revanche lorsqu’il sonne dans des lieux plus purs, il est plus aigu » (Jeauneau 1978, p. 18-119). |
| ↵30 | Voir les explications très détaillées de Teeuwen 2002, p. 228. |
| ↵31 | Voir encore I, 118, p. 353 ; ou I, 121, p. 359 : les sept mouvements de l’espace, deux en longueur vers l’avant et vers l’arrière, deux en largeur vers la droite et vers la gauche, deux en hauteur, vers le dessus ou le dessous : profunditas, sursum, deorsum, et le dernier autour d’un axe fixe, c’est-à-dire la rotation. Béatrice Bakhouche remarque (note 10 p. 723) qu’Aristote comme Martianus refusent la rotation à l’homme. Une étoile pour Calcidius n’a que deux de ces sept mouvements alors que Jean Scot, sans le dire clairement, les possibilités semblent plus ouvertes. |
| ↵32 | Lorsqu’elle le rencontre chez Jean Scot, Erika von Erhardt-Siebold est déconcertée par le mot (Erhardt-Siebold et Erhardt 1940, p. 13) : elle relève par exemple que Jean Scot dit « pro rationibus altitudinum seu descensionum » (Annotationes 11, 23). Toutefois, remarque-t-elle, « d’abord nous ne savons pas ce qu’il entend ici par altitudo et descensio, puisque l’Annotateur, comme Capella, utilise sans distinguer les mouvements de latitude de ceux qui concernent les profondeurs de l’espace ». Elle relève des occurrences qui vont dans le même sens, mais pourtant, dans ces relevés, on ne trouve pas le mot précis d’altitudo (Annotationes 433, 12, glose de « Alteriore » ; 450, 17, glose de « Paralleli », 467, 5 ; Lutz 1939). Sa difficulté n’est pas celle du mot mais celle de la compréhension des mouvements planétaires exacts. Une seule fois, dans les gloses du livre de l’Astronomie, le mot survient et il est défini : « altitudo est quando circulus alicuius planetae altius elevatur a terra », l’altitude désigne le moment où le cercle dessiné par quelque planète s’élève plus haut que la terre (Annotationes 467, 5, glose de « Et altitudinem » dans le livre de l’astrologie ; Lutz 1939). |
| ↵33 | Aucun commentateur n’a, à notre connaissance, expliqué l’étrangeté de cette quinte faite de trois tons entiers, d’autant qu’au-dessous du Soleil, la quinte supérieure est ensuite clairement détaillée, en ajoutant un cinquième son, celui des Fixes. La phrase suivante invite à penser que Saturne peut être très éloigné et qu’alors peut-être il faut ajouter le demi-ton qui manque. |
| ↵34 | Nous lisons spatia faciunt ou bien spatium facit. |
| ↵35 | Capella 2011, § 930, p. 30. Jean-Baptiste Guillaumin traduit par « un intervalle d’une grandeur bien définie » et insiste, dans son apparat critique, sur la polysémie du terme tonus. |
| ↵36 | Ilaria Ramelli traduit spiritus par intensità ; spisitudo et exilitas vocum par robustezza et delicatezza di voici. John MacInnis traduit spiritus par breath ; spisitudo et exilitas vocum par density ou sparseness of sounds. S’agirait-il d’une allusion à ce que notent les neumes ? |
| ↵37 | Expression apparemment obscure, mais qui décrit la manière d’obtenir et de comparer des rapports, des proportions, le fait qu’un même logos relie les termes entre eux, c’est-à-dire ce qui concerne les intervalles musicaux. Par exemple, dans le sens de la croissance et de l’extension, on passe de 1 à 2 (rapport double, d’octave) en ajoutant l’unité à l’unité ; puis de 2 à 3 (rapport sesquialtère, de quinte) en ajoutant la moitié de 2 à 2 ; puis on passe de 3 à 4 (rapport sesquitierce de quarte) en ajoutant un tiers de 3 à 3, etc. Les rapports diminuent, mais les nombres croissent, c’est une « ascension calculée », et ils s’étendent de sorte à rendre compte de l’ensemble du monde continu. Les rapports de rapports ou médiétés sont étudiés dans l’harmonique, et la médiété qu’est ici le Soleil en constitue l’articulation. La proportion double (octave) où il se situe est en effet la référence de tout, ce qui est rappelé au paragraphe précédent. |
| ↵38 | Nous lisons, comme MacInnis (2014, p. 125) crescendo au lieu de decrescendo. Mais notre traduction demeure générale et ne se réfère pas aussi explicitement que la sienne à la longueur d’une corde vibrante, dans la mesure où nous sommes bien ici dans des proportions qui augmentent ou diminuent et non pas dans des distances, même si la corde tendue est clairement le modèle de pensée (le paragraphe précédent parle bien d’extensio mais ajoute « selon la règle des nombres » [secundum regulas numerorum]). |
| ↵39 | Retour, en grec et en caractères romains dans le texte. |
| ↵40 | Nous lisons fortunarum, un mot que l’on retrouve chez Capella (2001, I, 11, 14, 15, p. 9, p. 11, p. 12, etc.). |
| ↵41 | Ibid., I, 14, p. 10. |